Vergleich des Schwingungsverhaltens: Schwingkreis-Dipol

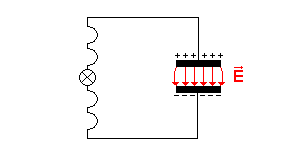
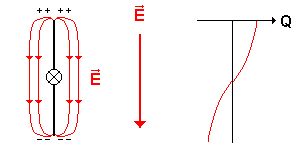
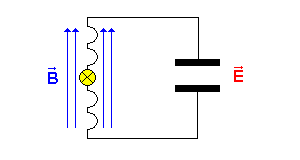
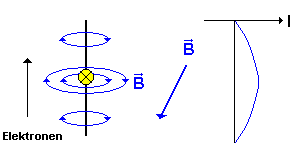
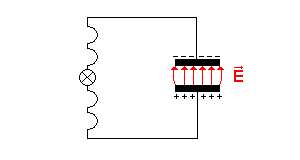
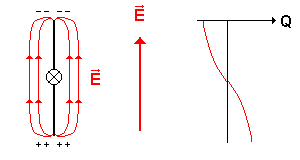
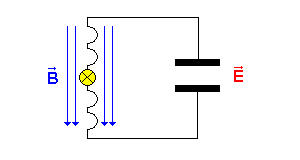
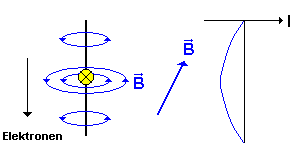
Für die ausgewählten Zeitpunkte t = 0 s , t = T / 4 , t = T / 2 und t = 3T / 4 wird hier der Schwingkreis und der Dipol verglichen.

Schwingkreis	Dipol
1.) t = 0 s: Maximale Ladung auf den Kondensatorplatten Maximales elektrisches Feld Kein Strom (Lampe dunkel) Kein magnetisches Feld Die gesamte Energie steckt im Feld des Kondensators	1.) t = 0 s: Maximale Ladung an den Dipolenden Maximales elektrisches Feld Kein Strom (Lampe dunkel) Kein magnetisches Feld Die gesamte Energie steckt im elektrischen Feld
2.) t = T / 4: Keine Ladung auf den Kondensatorplatten Kein elektrisches Feld Maximale Stromstärke (Lampe hell) Maximales magnetisches Feld Die gesamte Energie steckt im Magnetfeld der Spule	2.) t = T / 4: Keine Ladung an den Dipolenden Kein elektrisches Feld Maximale Stromstärke (Lampe hell) Maximales magnetisches Feld konzentrisch um die Dipolachse Die gesamte Energie steckt im Magnetfeld.
3.) t = T /2: Maximale Ladung auf den Kondensatorplatten Maximales elektrisches Feld Kein Strom (Lampe dunkel) Kein magnetisches Feld Die gesamte Energie steckt im Feld des Kondensators Polung und Orientierung des elektrischen Feldes ist umgekehrt wie bei 1.)	3.) t = T /2: Maximale Ladung an den Dipolenden Maximales elektrisches Feld Kein Strom (Lampe dunkel) Kein magnetisches Feld Die gesamte Energie steckt im elektrischen Feld Polung und Orientierung des elektrischen Feldes ist umgekehrt wie bei 1.)
4.) t = 3T / 4: Keine Ladung auf den Kondensatorplatten Kein elektrisches Feld Maximale Stromstärke (Lampe hell) Maximales magnetisches Feld Die gesamte Energie steckt im Magnetfeld der Spule Orientierung des magnetischen Feldes ist umgekehrt wie bei 2.)	4.) t = 3T / 4: Keine Ladung an den Dipolenden Kein elektrisches Feld Maximale Stromstärke (Lampe hell) Maximales magnetisches Feld Die gesamte Energie steckt im Magnetfeld Orientierung des magnetischen Feldes ist umgekehrt wie bei 2.)

Warum ein Dipol ein besonderer Schwingkreis ist, findet man hier.