Stehende elektromagnetische Wellen in Luft und Wasser.

1.) Der Sender für das Experiment.

Ein Röhrensender, der in vielen Sammlung vorhanden sein dürfte, strahlt eine elektromagnetische Welle mit einer Frequenz von ca. 436 MHz ab. Mit einem schnellen Frequenzzähler, wie er z.B. einmal bei ELV als Bausatz erhältlich war, kann man diese Frequenz sogar messen. Heute bietet ELV einen Frequenzzähler mit ähnlichen Daten für knapp 100 Euro unter der Bezeichnung FC 500 als Fertiggerät an. Auch als Bausatz ist das Gerät erhältlich.

Ein Sende- oder Empfangsdipol ist dann richtig abgestimmt, wenn er die Dipollänge Lambda / 2 hat. Die zu dem Gerät passenden Dipole haben eine Länge von ca. 32 cm. Also ist die Wellenlänge der abgestrahlten Welle (in Luft) etwa 64 cm.

Damit kann man die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle in Luft bestimmen:

Es gilt c = f* Lambda = 4,36*10⁸ 1/s * 0,62 m = 2,8 * 10⁸ m/s. Dies entspricht in etwa der Lichtgeschwindigkeit c.

2.) Eine stehende Welle in Luft.

Lässt man die elektromagnetische Welle gegen eine Metallplatte laufen, so werden die leicht beweglichen Elektronen in der Metallplatte zu Schwingungen angeregt. Diese Schwingungsfrequenz entspricht der Frequenz des Senders. Die Metallplatte wirkt also wie eine zweite Sendeantenne, die ihre Welle auch entgegen der ursprünglichen Welle aussendet. Zwischen dem Sender und der Metallwand bildet sich daher eine stehende Welle aus, deren Eigenschaften dieselben sind, wie bei einer stehenden mechanischen Querwelle oder einer stehenden Schallwelle.

Mit einem Empfangsdipol wird das Signal zwischen Sender und Metallwand empfangen und mit einer Diode gleichgerichtet. Man bekommt dann eine Spannung, die ein Maß für die elektrische Feldstärke am jeweiligen Messpunkt ist.

Direkt an der Metallwand ist eine Knotenstelle der elektrischen Feldstärke (Spannung minimal). Weitere Knotenstellen findet man in jeweils etwa 32 cm Abständen voneinander, also im Abstand Lambda / 2. Jeweils dazwischen erhält man Bauchstellen der elektromagnetischen Welle, hier wechselt die elektrische Feldstärke zwischen ihrem positiven und negativen Maximalwert hin und her - die Spannung wird maximal.

3.) Die Ausbreitungsgeschwindigkeit hängt vom Medium ab.

Nach der Theorie der Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle hängt diese vom Medium ab, in dem sich die Welle ausbreitet.
Für die Ausbreitungsgeschwindigkeit gilt:


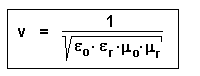
Im Vakuum (und näherungsweise auch in Luft) sind die Materialkonstanten Epsilon-r und My-r recht genau 1.

In Materie ist die Permeabilitätszahl My-r (außer bei Ferromagnetika) auch praktisch 1.
Die Dielektrizitätszahl hingegen ist meist größer als 1.
Folge: Die Ausbreitungsgeschwindigkeit von elektromagnetischen Wellen in Materie ist kleiner als in Luft. Damit ist auch die Wellenlänge kleiner als in Luft

Es gilt: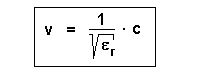

4.) Eine stehende Welle in Wasser.

Das Wassermolekül hat als polares Molekül eine recht hohe Dielektrizitätszahl von .
Das bedeutet, dass sich elektromagnetische Wellen in Wasser nur mit etwa 1/9 der Lichtgeschwindigkeit c ausbreiten sollten. Die Wellenlänge ist dann in Wasser ebenfalls nur etwa 1/9 der Wellenlänge in Luft.

Kann man dies experimentell überprüfen und beweisen?

Man kann das Experiment mit der stehenden Welle statt in Luft auch in Wasser durchführen. Der Sender steht vor einem Wassertrog, in dem sich destilliertes Wasser befindet. Am anderen Ende des Troges steht eine Metallplatte oder ein Spiegel (die reflektierende Spiegelschicht ist auch metallisch). Das nebenstehende Foto zeigt die Versuchsanordnung. Im Hintergrund sieht man den angepassten Messdipol und ein Spannungsmessgerät.

Der Empfangsdipol passt nicht!

Den "normalen" Empfangsdipol kann man zum Nachweis der elektromagnetischen Wellen in Wasser natürlich dann nicht mehr verwenden - er hat nicht die richtige Länge! Wenn die Wellenlänge in Wasser nur noch 1/9 der Wellenlänge in Luft beträgt, dann darf der "Wasserdipol" auch nur 1/9 der Länge des "Luftdipols" haben.

Eine Dipolhälfte des originalen "Luftdipols" (unten) und des angefertigten "Wasserdipols" (oben).

Wenn man keine passenden Dipole hat, dann muss man sie sich eben selber anfertigen! Dazu besorgt man sich im Baumarkt ein 1 m langes Aluminium Hohlrohr mit etwa 8 mm Außendurchmesser. Von dieser Stange werden zwei Stücke von etwa 2 cm Länge abgesägt (Foto). Anschließend drückt man jeweils eines der Enden mit einem Schraubstock auf etwa 6 bis 8 mm "platt" und bohrt dort mittig ein Loch von etwa 3 mm Durchmesser für die Befestigungsschraube am Dipol. .

Die original Dipolstangen werden dann durch die kurzen, selbstgemachten Dipolstangen ersetzt - der "Wasserdipol" ist einsatzbereit. Die Dipolstangen sind noch innerhalb des Kunststoffdeckels und ragen nicht über diesen hinaus (vgl. Foto). Der untere Teil wird ins Wasser eingetaucht - aber nicht zu tief, sonst läuft das Kunststoffgehäuse mit Wasser voll.

5.) Die Messung und ihre Ergebnisse.

Die Fotos zeigen das Ergebnis einer Messung, die im 4-stündigen Physikkurs 2006/2008 am Erich Kästner Gymnasium in Eislingen mit dem selbstgebastelten Dipol durchgeführt wurde.

Die erste Knotenstelle vor der Spiegelwand

Leider ist das Dipolgehäuse zu breit, man kommt nicht ganz an die reflektierende Spiegelfläche heran und kann daher die Knotenstelle der elektromagnetischen, stehenden Welle dort nicht nachweisen. Entfernt man den Empfangsdipol vom Spiegel, dann haben wir in etwa 5 cm Abstand eine weitere Knotenstelle gefunden, die zweite Knotenstelle entdeckten wir in ca. 12 cm Abstand (vgl. Fotos) Das Ergebnis ist nun Bestätigung und Enttäuschung zugleich! Bestätigung, weil der Versuch belegt, dass die Wellenlänge der elektromagnetischen Welle in Wasser tatsächlich deutlich kleiner als in Luft ist. Enttäuschung, weil man nach einer einfachen Theorie eine noch kleinere Wellenlänge erwartet hätte. Bei einer Wellenlänge von 64 cm in Luft und einer Dielektrizitätszahl von 81 müsste die Wellenlänge in Wasser 1/9 des Wertes von Luft also etwa 7 cm betragen (64 cm / 9). Tatsächlich messen wir aber als Wellenlänge etwa 12 cm, was einem Faktor 64 cm / 12 cm = 5,3 in den Ausbreitungsgeschwindigkeiten entspricht. Daraus errechnet sich die Dielektrizitätszahl zu etwa 28.

Die zweite Knotenstelle vor der Spiegelwand

Erklärung für die Abweichung.

Die Erklärung für die Abweichung liegt zunächst einmal darin, dass die Dielektrizitätszahl von Wasser nur im konstanten elektrischen Feld z.B. eines Plattenkondensators den Wert 81 hat. Die Wasserdipole richten sich dort perfekt aus.

Hat man es aber mit elektrischen Wechselfeldern zu tun, dann müssen die Dipole der Wassermoleküle ständig ihre Polung wechseln - und das ziemlich schnell.
Dass dies nicht so perfekt erfolgt, ist klar, daher sinkt bei elektrischen Wechselfeldern die Dielektrizitätszahl ab. Je größer die Frequenz, desto kleiner wird die Dielektrizitätszahl.

Man kann das schnelle Umpolen der Wassermoleküle sehr schön mit dieser Simulation der Universität von Colorado veranschaulichen.

6.) Vertiefende Hinweise zur Frequenzabhängigkeit der Dielektrizitätszahl von Wasser.

Auch Licht ist eine elektromagnetische Welle ( 10¹⁴ Hz) und gehorcht denselben Gesetzen. Die Brechung von Licht an einer Grenzschicht Luft-Wasser ist auf die unterschiedlichen Ausbreitungsgeschwindigkeiten der elektromagnetischen Lichtwelle in Luft und in Wasser zurückzuführen. ( vgl. hierzu diese Seite)

Dabei gilt für das Verhältnis von Einfallswinkel und Brechungswinkel:

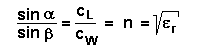
Führt man Brechungsversuche am Übergang Luft-Wasser mit Licht durch, so erhält man als Brechungsindex n etwa 1,3, das entspricht einer Dielektrizitätszahl von etwa 1,7.

Nimmt die Dielektrizitätszahl mit steigender Frequenz tatsächlich so drastisch ab?

Sieht man sich die einschlägige Hochschulliteratur an, so findet man dort, dass sich die Dielektritätszahl bei Frequenzen unter etwa 1 GHz gar nicht deutlich von denen in einem statischen Feld unterscheiden dürfte. Die Abhängigkeit der Dielektrizitätszahl von der Wassertemperatur ist hier z.B. deutlich drastischer als von der Frequenz.
(vgl. hierzu z.B. folgende Seite auf Englisch http://www.lsbu.ac.uk/water/microwave.html).

Wahrscheinlich ist die deutliche Abweichung nur so zu erklären, dass bei dem Experiment ein Teil des Dipols (die Diode zur Gleichrichtung und ihre Zuleitung) noch in Luft sind. Zu einem ähnlichen Ergebnis kommt auch die Firma Leybold in ihren Handreichungen zum bekannten Versuch "Dipole im Wassertank").
(vgl. hierzu http://www.leybold-didactic.com/literatur/hb/d/p3/p3724_d.pdf ).

Klaus-Dieter Grüninger, Landesbildungsserver