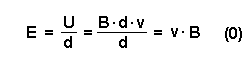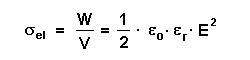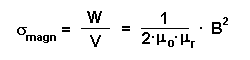Die Ausbreitungsgeschwindigkeit
einer elektromagnetischen Welle.

1.) Ein bewegtes Magnetfeld erzeugt ein elektrisches Feld.

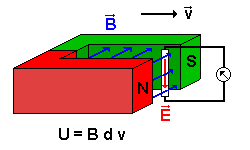Bewegt man einen Leiter im Feld eines Hufeisenmagneten, so wirkt die Lorentzkraft und es entsteht eine Induktionsspannung U = B*d*v. Man kann auch den Leiter ortsfest lassen und den Hufeisenmagneten bewegen, auch dann entsteht dieselbe Induktionsspannung und ein elektrisches Feld. Dieses Feld ist auch dann vorhanden, wenn gar kein Leiter im Hufeisenmagneten ist. Der Leiter stellt sozusagen nur die Elektronen bereit, die dazu nötig sind, das Feld nachzuweisen. Es gilt:

2.) Theoretische Betrachtung zur Energie eines elektrischen und eines magnetischen Feldes.

Elektrisches Feld (Plattenkondensator)	Magnetisches Feld (lange Spule)
Für die in einem Plattenkondensator gespeicherte Energie gilt: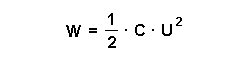 Dabei gilt für die Kapazität C: 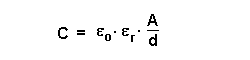Also folgt:	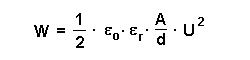Für die Energie in einer Spule gilt: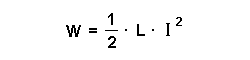 Dabei gilt für die Eigeninduktivität L: 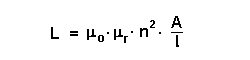Also folgt: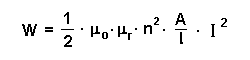
Zusammenhang: Spannung U - elektrische Feldstärke E	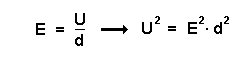Zusammenhang: Stromstärke I - magnetische Flussdichte B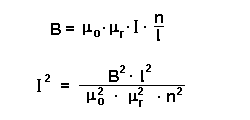
Damit ergibt sich: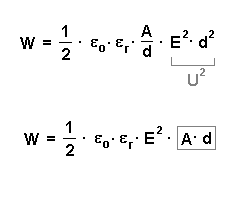	Damit ergibt sich: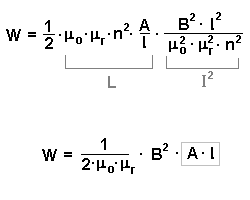
Das blau gezeichnete Quader-Volumen wird vom elektrischen Feld ausgefüllt:	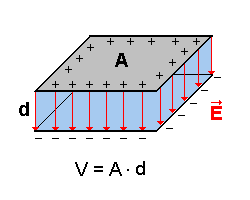Das blau gezeichnete Zylinder-Volumen wird vom magnetischen Feld ausgefüllt: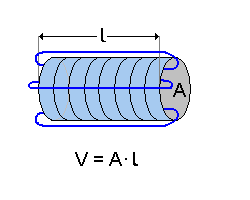
Für die elektrische Felddichte gilt:	Für die magnetische Felddichte gilt:

Elektrisches und magnetisches Feld kommen bei elektromagnetischen Wellen immer gemeinsam vor. Keines der beiden Felder dominiert das andere. Daher müssen die beiden Felddichten in einem elektromagnetischen Feld gleich groß sein und es gilt:

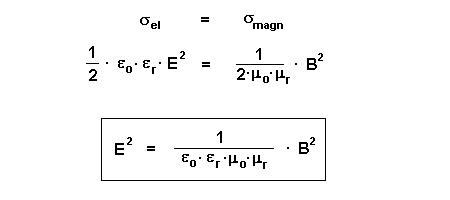
Durch Koeffizientenvergleich mit Gleichung (0) ganz oben auf dieser Seite ergibt sich für die Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle:

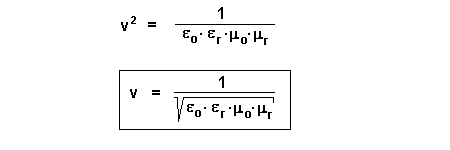
3.) Folgerungen aus der Gleichung :

1. Ausbreitungsgeschwindigkeit im Vakuum
   Im Vakuum und näherungsweise auch in Luft sind die Dielektrizitätszahl und die Permeabilitätszahl praktisch gleich 1.
   Es folgt daher:
   
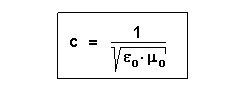
   Setzt man die elektrische und die magnetische Feldkonstante ein, so erhält man c = 2,99 * 10⁸ m/s.
   Dies entspricht der Lichtgeschwindigkeit.
   Elektromagnetische Wellen und auch Licht breiten sich im Vakuum mit der Lichtgeschwindigkeit c aus. Sie beträgt etwa 2,99 * 10⁸ m/s.
   
   
2. Ausbreitungsgeschwindigkeit in Materie
   Weil die Dielektrizitätszahl und die Permeabilitätszahl unter der Wurzel im Nenner stehen, ist die Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle in Materie vom Material abhängig.
   
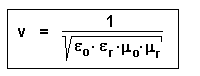
   Elektromagnetische Wellen breiten sich in Materie langsamer aus als im Vakuum.
   Dies kann man zeigen, wenn man eine stehende elektromagnetische Welle in Wasser nachweist.

Diese Seite gibt es auch als Arbeitsblatt (Word-Dokument) mit oder ohne Gleichungen zum Herunterladen:

Arbeitsblatt mit Formeln

Arbeitsblatt ohne Formeln

Klaus-Dieter Grüninger, Landesbildungsserver