Ausfall von Ordnungen.

1) Fehlt hier nicht etwas?

Sieh' dir das nebenstehende Interferenzbild genau an!

Richtig, bei der 2. Ordnung sieht das etwas seltsam aus. In der Mitte wird es statt hell plötzlich dunkel. Auch die 4. Ordnung zeigt die gleiche Erscheinung. Die erste und dritte Ordnung sind so wie erwartet.

Wie kommt es zu diesem seltsamen Phänomen?

2) Einzelspalt und Doppelspaltinterferenz zusammen bestimmen die Gesamtinterferenz.

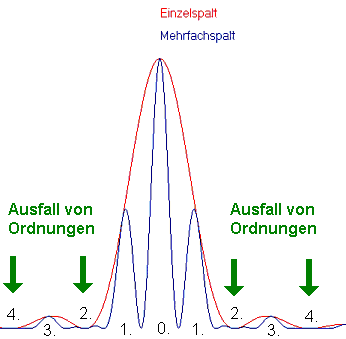Das Bild links zeigt die Verteilung der Lichtintensität zu dem Foto von oben.

Die Gesamtinterferenz setzt sich aus der Interferenz der beiden Spaltsysteme (Doppelspaltinterferenz blau) und auch der Interferenz innerhalb der einzelnen Spalte (Einzelspaltinterferenz rot) zusammen.

Eine Ordnung fällt immer dann aus, wenn ein Minimum der Einzelspaltinterferenz genau dorthin fällt, wo bei der Doppelspaltinterferenz eigentlich ein Maximum sein sollte.

Warum ist das so und unter welchen Umständen passiert das?

Sieh' dir die folgende Zusammenstellung an. Mehr zur Doppelspalt- und Einzelspaltinterferenz findest du, wenn du den Links in der Tabelle folgst.

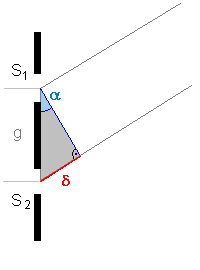
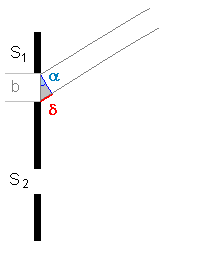
Maximum Doppelspaltinterferenz

Minimum Einzelspaltinterferenz

Ein Maximum beim Doppelspalt tritt immer dann auf, wenn der Gangunterschied δ (rot) der beiden (Mitten)Strahlen gerade ein ganzzahliges Vielfaches von λ ist.

Wenn dir nicht klar ist, warum das so ist, sieh' dir diese Webseite dazu an:

Interferenz beim Doppelspalt

Ein Minimum beim Einzelspalt tritt immer dann auf, wenn der Gangunterschied δ (rot) der beiden Randstrahlen gerade ein ganzzahliges Vielfaches von λ ist.

Wenn dir nicht klar ist, warum das so ist, sieh' dir diese Webseite dazu an:

Interferenz beim Einzelspalt

Für das k. Maximum der Doppelspaltinterferenz gilt also:
δ = k * λ

Nach der Geometrie von oben gilt dann:
sin α = δ / g = k * λ/g

Für das n.Minimum der Einzelspaltinterferenz gilt also:
δ = n * λ

Nach der Geometrie von oben gilt dann:
sin α = δ / b = n * λ/b

Eine Ordnung fällt immer dann aus, wenn ein Einzelspaltminimum in die gleiche Richtung fällt wie ein Doppelspaltmaximum, d.h. wenn die beiden Winkel α gleich sind.

Dann folgt:

k * λ/g = sin α = n * λ/b

Auf beiden Seiten des Gleichheitszeichens steht λ, das kann man also kürzen.
Physikalisch bedeutet dies, dass der Ausfall von Ordnungen nicht von der Wellenlänge abhängt. Fällt z.B. bei rotem Licht jede zweite Ordnung aus, dann ist dies auch bei grünem und blauem Licht so!

Weiter vereinfacht ergibt sich also:

k / g = n / b

oder umgeformt:

k / n = g / b

Beim Bild oben fällt das zweite Maximum der Doppelspaltinterferenz (k = 2) genau auf das erste Minimum der Einzelspaltinterferenz (n = 1). Die Spaltbreite b beim verwendeten Doppelspalt ist b = 0,05 mm, der Spaltmittenabstand g ist g = 0,1 mm. Oben eingesetzt ergeben die Quotienten auf beiden Seiten (k / n) bzw. (g / b) gerade 2.
Dies ist auch der Fall, wenn das vierte Maximum der Doppelspaltinterferenz (k = 4) auf das zweite Minimum der Einzelspaltinterferenz (n = 2) fällt.
Mit anderen Worten, es fällt hier jede zweite Doppelspaltinterferenz aus, weil g gerade 2*b ist.

Daraus kann man schließen:

Ist der Spaltmittenabstand g ein x-faches Vielfaches des Spaltbreite b, so fällt jedes x. Maximum des Doppelspalts aus.

Wäre also z.B. die Spaltbreite b = 0,05 mm und der Spaltmittenabstand g = 0,15 mm, so würde jedes dritte Doppelspaltmaximum (3., 6., 9.) ausfallen.