Begrenzte Zahl an Ordnungen.

Bevor diese Frage erörtert wird, soll hier zunächst einmal eine Vorüberlegung angestellt werden.
Lies sie dennoch durch, nur so kannst du das Problem völlig verstehen.

1) Das Interferenzdreieck entscheidet über den Winkel.

Tobias hat einen roten Laserpointer geschenkt bekommen und möchte damit Zuhause die Interferenzversuche aus dem Physikunterricht nachstellen. Er berußt eine kleine Glasscheibe mit einer Kerze, und kratzt im Abstand von etwa 2 mm mit einem spitzen Bleistift zwei Spalte in den Ruß. Als er seine Anordnung mit dem Laserpointer beleuchtet und an der Zimmerwand beobachten möchte, ist er enttäuscht - es ist keine richtige Interferenzerscheinung zu sehen.
  • Was hat Tobias falsch gemacht, bzw. was hat er nicht bedacht?
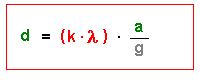{short description of image} Überlegen wir die Gründe am Beispiel des Maximums 1. Ordnung:
Zunächst einmal ist Tobias' Zimmer vielleicht zu klein. Um die Interferenzerscheinung gut trennen zu können, sollte der Schirmabstand a (Abstand Glasplatte - Wand) nicht zu klein sein, sonst wird die Auftrennung d nicht groß genug.
  • Aber selbst wenn sein Zimmer deutlich größer wäre, würde er keinen Erfolg haben. Warum?
  • Bekommt man eigentlich bei jedem Doppelspaltabstand g eine "brauchbare" Interferenz, die man gut beobachten kann?
Das Interferenzdreieck entscheidet

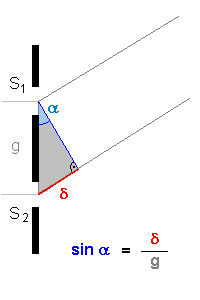
Betrachten wir dazu das Interferenzdreieck. Über den Winkel α , unter dem das Maximum 1.Ordnung zu sehen sein wird, entscheiden zwei Größen:

  • Der Spaltabstand g der beiden Spalte.
  • Der Gangunterschied δ der beiden interferierenden Wellen.
    Er ist für das Maximum 1. Ordnung gerade die Wellenlänge λ.

Für eine brauchbare Interferenz müssen Spaltabstand g und Wellenlänge zusammenpassen.
Die Wellenlänge des Lichts ist je nach Lichtfarbe 400 nm bis 800 nm.
Tobias' roter Laserpointer dürfte eine Wellenlänge von etwa 650 nm haben.
  • Unter welchem Winkel wird das Maximum 1.Ordnung bei Tobias auftreten? (Wir rechnen nach)

Es gilt: sin α = δ / g. Für die erste Ordnung ist δ = 1*λ

Also folgt sin α = 1*λ / g = 6,5*10-7 m / 2*10-3 m = 3,25*10-4.
Das ergibt einen Winkel von etwa 0,018°.
Wenn man für kleine Winkel (und das ist definitiv einer!) sin α = tan α setzen darf, dann ist d = a * tan α = 3,0 m * 0,00035 = 0,000975 m ,d.h. knapp 1 mm für einen Wandabstand von 3,0 m!

Kein Wunder, dass Tobias das nicht beobachten konnte.

Für "brauchbare" Winkel muss also der Abstand g der beiden Spalte deutlich kleiner sein.
Bei einem Spaltabstand von 0,1 mm (1*10-4 m) beträgt der Winkel dann schon 0,37° und der Abstand der 1. Ordnung zur Mitte wäre (bei gleicher Schirmentfernung von 3,0 m) knapp 2 cm - das hätte Tobias in seinem Zimmer sicher sehen können.

Doch auch bei diesem feinen Spalt ist der Spaltabstand g immer noch mehr als einen Faktor 100 größer als die Lichtwellenlänge!

2) Sehr kleine Spaltabstände führen zu neuen Erscheinungen.

  • Müsste es nicht noch besser gehen, wenn man die Spaltabstände noch viel kleiner macht, insbesondere wenn der Spaltabstand in der Größenordnung der Wellenlänge liegt?

Für seine weiteren Forschungen leiht sich Tobias von seinem Physiklehrer ein Gitter mit 570 Strichen je mm aus.
Hier ist der Abstand zweier benachbarter Spalte also 1 / 570 mm = 0,00175 mm = 1,75*10-6 m.
Das ist nur etwa das Doppelte der Wellenlänge des roten Laserlichts!

Wieder erlebt Tobias eine Überraschung. Er sieht deutlich das Zentralmaximum, aber wo ist das Maximum 1. Ordnung?
Nach einigem Suchen entdeckt er es an seinem Kleiderschrank.

Dann rechnet er nach:
sin α = 1*λ / g = 6,5*10-7 m / 1,75*10-6 m = 0,371. Das ergibt einen Winkel von immerhin 21,8°.

Klar, dass man hier die Näherung sin α = tan α nicht mehr benutzen darf!
Tan 21,8° ist ziemlich genau 0,4. Damit ist d = a * tan(21,8°) = 1,2 m.

  • Tobias geht mit der Anordnung näher an die Wand.
    Warum sieht er hier aber nur 5 Punkte?
    Neben dem Zentralmaximum in der Mitte gibt es nur zwei weitere Ordnungen.
    Warum?
 Es sind nur zwei Ordnungen zu sehen
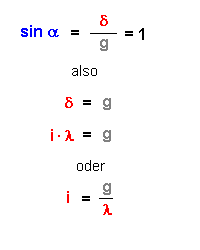{short description of image} Da Tobias vorher ja gerechnet hatte, kann er sich diese Frage schnell selber beantworten:
Für die zweite Ordnung wird der Winkel ja noch größer und für die dritte Ordnung abermals größer.

Größer als 90° kann der Winkel α aber nicht werden, dann ist der Sinus des Winkels 1.
  • Bis zu welcher Ordnung i wird es also gehen (i wird jetzt sicher keine gerade Zahl)?

i = g / λ = 1,75*10-6 m / 6,5*10-7 m = 2,69.
Die Zahl der Ordnungen, die tatsächlich auftreten, ist die nächst kleinere ganze Zahl, in diesem Falle also 2.
Er sieht also das Zentralmaximum und erste und zweite Ordnung jeweils links und rechts davon, insgesamt also fünf Lichtflecke.

Aufgabe:
In der Physiksammlung gibt es auch noch ein anderes Gitter mit 300 Spalten je mm.
Wieviele Ordnungen werden in diesem Fall zu sehen sein, wenn man grünes Laserlicht (535 nm) verwendet?

Hier siehst du zwei Fotos, die den Blick auf die Anordnung zeigen. Der Schirmabstand ist bei beiden Versuchen gleich.

Welches Foto gehört zum Gitter mit 570 Spalten je mm und welches zum Gitter mit 300 Strichen je mm ?
Hast du die Zahl der Ordnungen für das 300 Spalten je mm Gitter richtig vorhergesagt (Aufgabe)?

Das 570 Striche je mm Gitter Das 300 Striche je mm Gitter
Die Staubpartikel zeigen wo konstruktive Interferenz passiert

Besonders schön kann man die großen Winkel erkennen, wenn man in den Raum zwischen Gitter und Schirm streuende Partikel, etwa Kreidestaub oder Zigarettenrauch bringt. Das nebenstehende Bild zeigt die Interferenzerscheinung beim 570 Spalte je mm Gitter - von oben fotografiert. Die Streupartikel sind Kreidestaub (Tafellappen).

Für die Aufnahmen wurde ein 100 mW Grünlaser benutzt. Solche Laser sind für den Einsatz im Unterricht nicht zugelassen. Hier dürfen nur Laser der Klasse I (bis 1 mW) Verwendung finden.
Man kann die gleichen Versuche aber auch mit solchen Lasern machen. Das menschliche Auge ist empfindlicher als die Kamera.

Fotos, Grafiken und Seite: Grüninger, Landesbildungserver