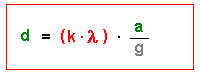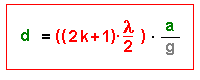Interferenz beim Doppelspalt.

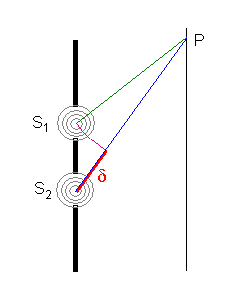
In einem Spalt entstehen Elementarwellen. Wir betrachten hier zwei Spalte (oder Quellen) S1 und S2 in denen jeweils eine Elementarwelle entstehen soll. Diese Elementarwellen überlagern sich. Uns interessiert dabei die Interferenz an einem Punkt P (z.B. auf einem Schirm).

Elementarwellen und Wellenstrahlen Dazu betrachten wir diejenigen Wellenstrahlen(d.h. die Senkrechten auf den Wellenfronten), welche die Spalte S1 und S2 jeweils mit dem Punkt P verbinden.

Dabei ist der grüne Wellenstrahl von S1 nach P offensichtlich kürzer als der blaue Wellenstrahl von S2 nach P. Auf den blauen Wellenstrahl passen also mehr Wellenlängen als auf den grünen Wellenstrahl.

Es ergibt sich die rot gezeichnete Streckendifferenz δ, die man auch die Gangdifferenz oder den Gangunterschied nennt.

1) Der Gangunterschied bestimmt die Interferenz.

Wie die beiden Wellen nun miteinander interferieren, hängt von diesem Gangunterschied ab.
Folgende Sonderfälle sind zu unterscheiden:

  • Der Gangunterschied δ ist ein ganzzahliges Vielfaches der Wellenlänge λ :

    Anschaulich bedeutet das z.B. für Wasserwellen, dass gerade 1, 2, 3, 4,... Wellenlängen λ auf die Strecke δ passen.

    Allgemein gilt : δ = k * λ ( mit k = 0, 1, 2, 3, 4, ...)

    Dann fallen im Punkt P die Wellenberge und Wellentäler der beiden in S1 und S2 entstandenen Elementarwellen aufeinander und verstärken sich (konstruktive Interferenz).
    Im Punkt P entsteht deshalb also ein Maximum.
    Dies gilt auch für andere Querwellen (wie z.B. elektromagnetische Wellen und Licht). Man würde dort zwar anders argumentieren (mit den Vektoren der elektrischen Feldstärke, die dort gleichgerichtet sind), das Ergebnis bleibt das gleiche, es entsteht ein Maximum, bei Lichtwellen also Helligkeit.

  • Der Gangunterschied δ ist ein ungeradzahliges Vielfaches der halben Wellenlänge λ / 2 :

    Anschaulich bedeutet das z.B. für Wasserwellen, dass gerade 1/2 , 3/2 , 5/2 , 7/2, ... Wellenlängen auf die Strecke δ passen.

    Allgemein gilt : δ = (2*k +1) * λ / 2 ( mit k = 0, 1, 2, 3, 4, ...)

    In diesem Fall fällt daher im Punkt P ein Wellenberg der Welle von S1 auf ein Wellental der Welle von S2. Die beiden Wellen heben sich auf (destruktive Interferenz).
    Im Punkt P entsteht in diesem Falle ein Minimum.
    Bei Lichtwellen (Vektoren der elektrischen Feldstärke entgegengesetzt) ergibt sich dann also in P Dunkelheit.

2) Die Geometrie kommt ins Spiel - das Lagedreieck.

Nun kann der Punkt P überall auf dem Schirm liegen und der Schirm kann sich auch in ganz verschiedenen Entfernungen a von den beiden Spalten entfernt befinden. All dies entscheidet sicher darüber, wie die beiden Wellen aus S1 und S2 in diesem Punkt interferieren.

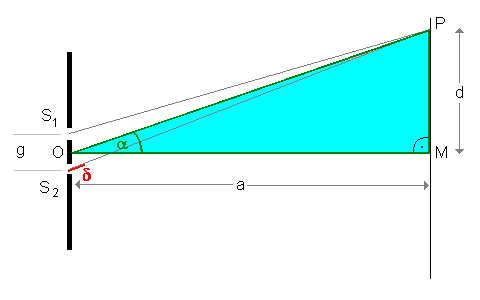Das Lagedreieck Im grünen, rechtwinkligen Dreieck gilt offenbar folgende Beziehung:

tan α = d / a
(1)

Je weiter der Punkt P oberhalb (oder auch unterhalb) der Verbindungslinie OM liegt, desto größer ist der Gangunterschied δ und desto größer wird auch der Winkel α.

Sonderfall:
Interferieren die Wellen in M (P liegt auf M -> d und α sind dann 0), so gibt es keinen Gangunterschied. Hier interferieren die Wellen ebenfalls konstruktiv, wir bekommen das Haupt- oder Zentralmaximum. Dies gilt auch für jeden anderen Punkt auf der Verbindungslinie OM und damit für jeden beliebigen Schirmabstand a.

3) Die Verhältnisse werden richtig gestellt!

Für Versuche mit Licht ist die Zeichnung von oben natürlich überhaupt nicht maßstabsgetreu. In der Praxis arbeiten wir hier mit Spaltabständen g in der Größenordnung von 1 mm oder weniger, die Schirmabstände a sind in der Größenordnung von einigen Metern und wir untersuchen die Interferenz zentrumsnah, d.h. die Strecke d beträgt einige Zentimeter.

Das hat Folgen:

  • Der Winkel α ist also nicht (wie in der Zeichnung) vielleicht 30°, sondern liegt in Wirklichkeit im Bereich von 1°!
    Die Winkel α sind also sehr klein.

  • Die Schirmentfernung a ist in Wirklichkeit um etwa einen Faktor 1000 bis 10000 größer als der Spaltabstand g!
    Wollte man die Verhältnisse auf deinem Bildschirm also richtig darstellen und der Abstand a wäre deine Bildschirmbreite, dann wären die beiden Spalte S1 und S2 gerade mal ein Pixel (einen Bildpunkt) oder weniger auseinander!

  • Die beiden Wellenstrahlen von S1 und S2 nach P verlaufen in Wirklichkeit fast parallel.

Stelle dir als Modell vor, du stehst auf einer schnurgeraden, stillgelegten Eisenbahnstrecke mitten auf dem Gleis, du stehst dann im Punkt O. Die beiden parallelen Schienen sind die beiden Wellenstrahlen, sie sind etwa 1,5 m auseinander. Im richtigen Maßstab liegt der Punkt P dann in einigen Kilometern Entfernung - praktisch am Horizont. Du hast den Eindruck, die beiden Schienen laufen dort zusammen.

Die Entfernung wird veranschaulicht

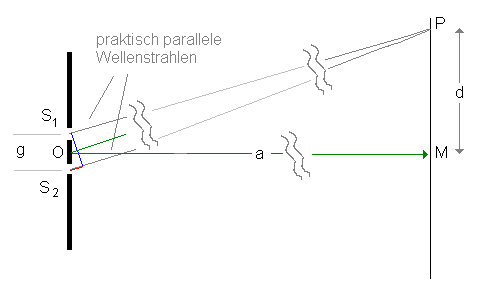Die nächste Skizze soll diese Idee verdeutlichen. Der rechte Teil der Zeichnung (rechts von den geschwungenen Bögen mit Schirm und den Punkten P und M) müsste also im richtigen Maßstab mehrere Meter rechts von dir liegen!

Das spielt für die weiteren Betrachtungen aber gar keine Rolle, denn wir wollen uns nun auf das kleine Dreieck direkt neben den beiden Spalten konzentrieren.
Das wird noch einmal heraus vergrößert.

Ein Teil des grünen Dreiecks OMP von oben wurde auch noch einmal eingezeichnet.
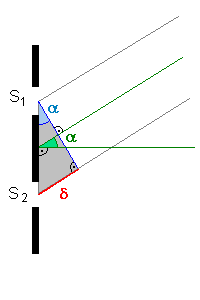Gleiche Winkel in beiden Dreiecken Man erkennt, dass der Winkel α des grünen Lagedreiecks aus 2) auch in dem grauen, rechtwinkligen Interferenzdreieck an der Spitze oben (blau eingezeichnet) noch einmal vorkommt. Die untere, rote Strecke ist der Gangunterschied δ der beiden Wellenstrahlen zum Punkt P.
Natürlich sind auch hier in der Darstellung die Winkel wieder maßlos übertrieben:
in Wirklichkeit sind sie in der Größenordnung von 1°! (s.o.)

Konzentrieren wir uns nun auf das Interferenzdreieck und lassen den Bezug zum grünen Lagedreieck weg.

4) Das Interferenzdreieck.

Das Interferenzdreieck 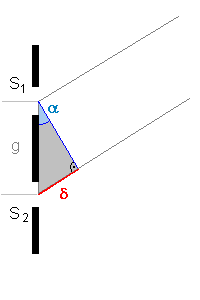Im rechtwinkligen Interferenzdreieck ist der Gangunterschied δ die Gegenkatete zum Winkel α und der Abstand der Spaltmitten g (oft nur - etwas ungenau - Spaltabstand genannt) die Hypotenuse.

Es gilt also folgende Beziehung:

sin α = δ / g
(2)

Es wird Zeit unsere Überlegungen zusammenzufassen....

5) Zusammenfassung der Überlegungen:


Zusammenfassung der Ergebnisse

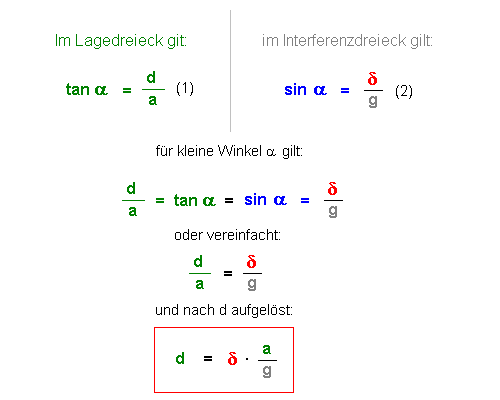
Entsprechend der Überlegungen aus 1) für welche Gangunterschiede sich Maxima (Helligkeit) bzw. Minima (Dunkelheit) ergeben, folgt daraus:

Maxima (Helligkeiten) ergeben sich wenn gilt: Bedingung für Maxima (k = 0, 1, 2, 3, 4,...)
Minima (Dunkelheiten) ergeben sich wenn gilt: Bedingung für Minima (k = 0, 1, 2, 3, 4,...)

Beachte:

Diese Näherungsgleichungen gelten gemäß ihrer Herleitung nur, solange die Winkel α noch sehr klein (< 5°) sind.

Hat man Doppelspalte, bei denen der Spaltmittenabstand g in etwa in der Größenordnung der Wellenlänge λ des Lichts liegen, dann kann man diese Näherungsgleichungen meist nicht mehr verwenden.

Der Rechenweg, zunächst über eine der Gleichungen (1) oder (2) den Winkel α zu berechnen und danach mit der anderen Gleichung zum Ergebnis zu kommen, geht dann aber immer noch.

Genau die gleiche Herleitung kann man auch für die Interferenz beim Gitter verwenden, es gelten dort auch dieselben Gleichungen.

Der Spaltmittenabstand g heißt dann dort Gitterkonstante g(daher kommt auch der Buchstabe g für den Spaltmittenabstand).

Statt zweier Wellen interferieren dort eben viele Wellen miteinander.
Jeweils zwei benachbarte Wellen haben dann aber immer noch jeweils den gleichen Gangunterschied zueinander.

Seite und alle Grafiken: Grüninger, Landesbildungsserver, 2013