Interferenz beim Einzelspalt.

1) Es kommt anders als man denkt .....

Trifft eine Wellenfront bei der Wasserwellenwanne auf einen Spalt, so entsteht dort eine neue Elementarwelle. Man beobachtet die Welle nicht nur in der "Geradeausrichtung", sondern auch seitlich - die Welle wird gebeugt.

Bild Wellenwanne Beugung

• Was erwarten wir, wenn wir Licht(wellen) auf einen sehr schmalen Spalt treffen lassen?

Man würde wahrscheinlich erwarten, dass auch hier Licht seitlich vom Spalt auftrifft, dass man also auf der ganzen Schirmbreite Helligkeit bekommt.

Führt man jedoch das Experiment durch, so erlebt man eine Überraschung!

Man bekommt kein durchgängiges Lichtband, sondern dazwischen sind immer wieder Dunkelstellen zu beobachten (vgl. Bild).
Diese Dunkelstellen können aber nur dadurch entstehen, dass mehrere Elementarwellen destruktiv miteinander interferieren.
Im Spalt muss also mehr als eine Elemenarwelle entstehen.

2) Spalt oder Scheunentor? - Eine Frage der Wellenlänge und der Spaltbreite.

• Warum hat man bei der Wasserwellenwanne nichts von einer solchen destruktiven Interferenz bemerkt?

Bei der Wasserwellenwanne liegt die Wellenlänge der Wasserwellen in der Größenordnung von 1 cm. Die Breite der Spalte ist etwa ebenso groß. Im Spalt kann man also tatsächlich eine Elementarwelle entstehen.

Bei Licht ist die Situation völlig anders: die Wellenlängen des Lichts betragen je nach Lichtfarbe 800 nm bis 400 nm, nehmen wir für eine Abschätzung 500 nm an, dies sind 5*10^-7 m. Ein Spalt möge die Breite 0,5 mm oder 5*10^-4 m haben.
Das bedeutet, dass die Spaltbreite um einen Faktor 1000 größer ist als die Wellenlänge des Lichts!
Der Spalt ist - aus der Sicht der Lichtwellen - also eher ein "Scheunentor"!
Im Spalt entsteht daher nicht nur eine Elementarwelle sondern sehr viele Elementarwellen, die alle miteinander interferieren. Selbst in einem sehr engen Spalt von 0,05 mm entstehen dann immer noch etwa 100 Elementarwellen.

2) Der Umgang mit dem Chaos.

Nun haben wir zwei Probleme:

• Wir wissen gar nicht, wie viele Elementarwellen konkret im Spalt entstehen.
• Jede Elementarwelle kann mit jeder interferieren, was die Sache kompliziert macht.

Wir müssen also eine passende Strategie finden.

Der Mathematiker Carl Friedrich Gauß hat angeblich als Grundschüler von seinem Lehrer die Aufgabe bekommen die Zahlen von 1 bis 100 zu addieren. Statt aber 1 + 2 + 3 +.... zu rechnen, hat sich Gauß nach "passenden Paaren" umgesehen: 1 + 100 ; 2 + 99; 3 + 98 usw. - so konnte er die Aufgabe sehr schnell lösen!

Wir können ähnlich vorgehen und uns nach passenden Paaren von Elementarwellen umsehen, die sich jeweils durch destruktive Interferenz gegenseitig auslöschen!

Nehmen wir an, in einem Spalt entstehen 100 Elementarwellen, unter welchen Umständen interferieren sie alle destruktiv miteinander?

Die erste Idee wäre vielleicht (ähnlich wie Gauß) die Wellenstrahlen von Welle 1 und 100 zu "koppeln" und zu sagen, diese Randstrahlen löschen sich aus, wenn ihre Gangdifferenz λ / 2 beträgt.
Das passt dann zwar für diese beiden Wellen, aber Welle 50 und Welle 51 in der Mitte sind nahezu phasengleich und würden sich verstärken. Das kann also insgesamt zu keiner destruktiven Interferenz aller Wellen führen!

Wir müssen also nach passenderen Paaren suchen!

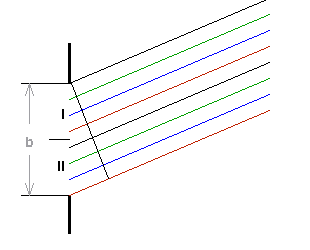
Teilen wir die Wellenstrahlen in zwei Teilbündel: Wellenstrahl 1 bis 50 (oben) in Teilbündel I und Wellenstrahl 51 bis 100 (unten) in Teilbündel II.
Wenn Wellenstrahl 1 und Wellenstrahl 51 (Mitte) gerade eine Gangdifferenz von λ / 2 haben, dann löschen sie sich aus.
Dann haben aber auch die Wellenstrahlen 2 und 52, 3 und 53, 4 und 54 .... 50 und 100 gerade einen Gangunterschied von λ / 2!
Wir haben so die passenden Paare gefunden, die sich jeweils gegenseitig auslöschen.

Die Gangdifferenz der Wellenstrahlen vom oberen Rand bis zur Mitte ist dann λ / 2, vom oberen Rand zum unteren Rand (Randstrahlen) ist sie dann λ.

Diese Überlegung der passenden Paare ist unabhängig von der Zahl der im Spalt entstehenden Elementarwellen. Würden wir 8 Elementarwellen annehmen, dann wären die Wellenstrahlen 1 bis 4 im ersten Bündel I und Wellenstrahlen 5 bis 8 im zweiten Bündel II. Man "koppelt" dann 1 und 5 (schwarz), 2 und 6 (grün), 3 und 7 (blau) sowie 4 und 8 (rot). Bei 1000 Elementarwellen umfasst das erste Bündel eben die Wellenstrahlen 1 bis 500 und das zweite Bündel 501 bis 1000. Diesmal koppelt man 1 und 501, 2 und 502, ... 500 und 1000. Die Überlegung bleibt stets die gleiche!

Und was passiert, wenn die Zahl der entstehenden Elementarwellen ungerade ist?

Nun, dann hat eine Elementarwelle eben keinen "Partner", der mit ihr destruktiv interferiert. Diese Welle bringt eine gewisse Resthelligkeit auf den Schirm. Diese ist aber (bei z.B. 1001 entstehenden Wellen) so gering, dass wir sie mit dem Auge gar nicht wahrnehmen können!

3) Die Interferenz mit Phasenzeigern verdeutlicht.

Man kann Interferenz verschiedener Elementarwellen auch mit Phasenzeigern verdeutlichen. Wie beim Doppelspalt und bei den Mehrfachspalten setzt man dabei den jeweils nächsten Phasenzeiger unter einem entsprechenden Phasenwinkel an die Spitze des vorhergehenden Zeigers.

In der folgenden Simulation wird von 8 Elementarwellen ausgegangen, um den Überblick noch behalten zu können. "Partnerstrahlen" (im Sinne der geeigneten Paarbildung von oben) haben jeweils die gleiche Farbe.

Fragen und Aufgaben:

• Wie liegen die Phasenzeiger aller 8 Elementarwellen, wenn die Phasendifferenz 0° ist?

Aktiviere die Auswahlbox "Zeichnen - Hilfslinien der Winkel"
Ändere die Phasenwinkel auf verschiedene Winkel zwischen 10° , 20° und 30°.

• Mache dir die Winkelbeziehungen zwischen den einzelnen Phasenzeigern klar.

Wähle als Phasenwinkel 22,5°.

• Welche Phasendifferenz haben der 1. und 5. Strahl?
• Wie sieht man das im Phasendiagramm?
• Welche Phasendifferenzen haben die beiden schwarzen, grünen, blauen und roten Zeiger jeweils?

Stelle nun 45° als Phasenwinkel ein.

• Welche Phasendifferenz hat der 1. und 5. Strahl nun?
• Was ist dies als Bruchteil der Wellenlänge λ ausgedrückt?
• Was kann man über die jeweils gekoppelten schwarzen, grünen, blauen und roten Phasenzeiger aussagen?
• Welche Länge hat nun der Summenzeiger? Was bedeutet das?
• Welche Phasendifferenz und welche Gangdifferenz ergeben sich bei 45° zwischen den Rändern des Spalts?

Wähle nun Phasenwinkel größer als 45°.

• Bei welchem Phasenwinkel heben sich wieder alle Phasenzeicher auf?
• Welcher Phasenwinkel und welche Gangdifferenz liegt nun zwischen dem 1. und 5. Strahl?
• Welcher Phasenwinkel und welche Gangdifferenz ergibt sich zwischen den Rändern des Spalts?

Fotos, Grafiken und Simulation: Grüninger, Landesbildungsserver