C) Allgemeiner Punkt im zweidimensionalen Wellenfeld.

Bisher haben wir uns auf ganz spezielle Punkte in unserem Wellenfeld beschränkt.
Kann man nicht für jeden beliebigen Punkt des Wellenfeldes eine solche Überlegung anstellen?
Wie müsste man dazu vorgehen?

(1) Von Wegstrecken und Phasenwinkeln.

Wir hatten gesehen, dass es für die Interferenz wichtig ist, welche Wegstrecke die Wellen bis zu dem Punkt P zurücklegen. Dies bestimmt den Phasenwinkel der Welle am Ort P.

Ein Beispiel:

Vom Errreger E1 zum Punkt P sind es 2,5 cm. Die Wellenlänge beträgt 2 cm.
Also "passen" gerade 2,5cm / 2cm also 1,25 Wellenzüge auf diese Strecke.

Der "Nachkomma-Anteil" ist nun für den Phasenwinkel wichtig.

Zu einer ganzen Wellenlänge gehört der Phasenwinkel 360 Grad (im Bogenmaß 2* π), also gehört zu 0,25 Wellenlängen der Phasenwinkel 90 Grad (π/ 2).
Der Punkt P "schwingt" also im Verhältnis zum Erreger um 90 Grad phasenverschoben.

(2) Erst die Überlagerung macht's.

Für die Interferenz ist dann noch wichtig, mit welchem Phasenwinkel die vom Erreger E2 erzeugte Welle in P ankommt.

Sind beide Wellen phasengleich verstärken sie sich maximal, sind sie in Gegenphase (Winkel 180 Grad) heben sie sich genau auf.

Bei anderen Phasenwinkeln muß man die Gesamtphase durch Verktoradditon ermitteln. Man erhält dann die Maximalamplitude und den Phasenwinkel der Überlagerung.

Wieder ein Beispiel:

Vom Erreger E2 zum Punkt P sind es 2,8 cm. Die Wellenlänge ist dieselbe wie für den Erreger E1
Die Zahl der Wellenzüge ist dann: 2,8cm / 2,0cm = 1,4.
Der Phasenwinkel ist dann 0,4 * 360 Grad = 144 Grad.

Um die maximale Gesamtamplitude zu bekommen, muß man nun einfach die beiden Phasenzeiger auftragen und vektoriell addieren. Die Länge der Phasenzeiger-Pfeile sind die Amplituden der Wellen. Die Länge des Summenvektors entspricht der Gesamtamplitude.

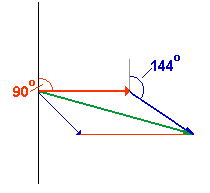(3) Und nun wieder zeitabhängig.

Wenn die Erreger gerade beim Phasenwinkel 0 Grad sind (maximale Auslenkung nach oben), dann ist das Dreieck der Phasenzeiger genau in der oben gezeichneten Position.

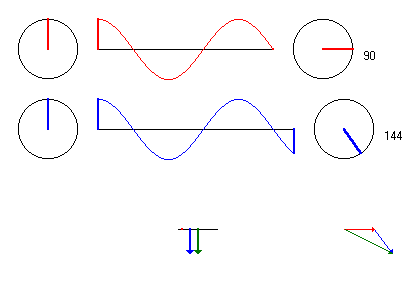Möchte man das Ganze wieder zeitabhänigig haben, muß man nur das ganze Dreieck mit festen Winkeln im Kreis rotieren lassen.
Die aktuelle Auslenkung des Punktes P ist dann jeweils wieder die Projektion des Summenzeigers auf die Senkrechte.

Die folgende Animation ist für dieses Beispiel gerechnet. (Beachte das feste Gerüst der rotierenden Zeiger unten rechts)

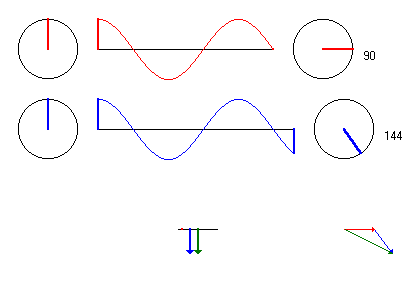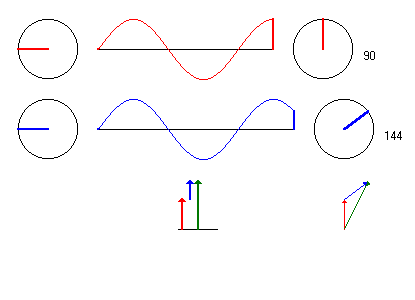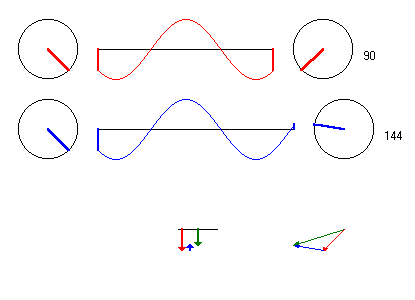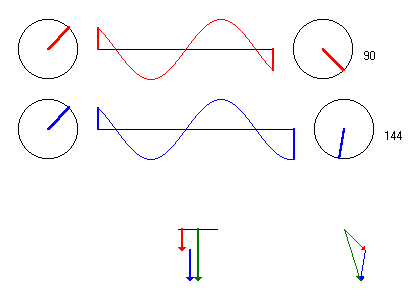
Na, vollen Durchblick gewonnen?
Ich hoffe doch, falls nein, arbeite die Seiten einfach noch einmal durch!
Wenn Du diese Gedanken verstanden hast, ist es bis zum Doppelspalt nur ein kleiner Schritt.

(4) Noch mehr zum Thema.

Die Animationen wurden mit einem Delphi-Programm berechnet, und dann die Screenshots als animierte Grafik zusammengepackt. Das Programm kannst du hier herunterladen.

Wenn Du den Oberstufenband von Dorn Bader als Physikbuch hast, kennst Du vielleicht die Darstellung des zweidimensionalen Wellenfeldes von S. 179. Das Programm von Herrn Wegner dazu kannst du ebenfalls hier laden.

Es rechnet von oben nach unten alle Punkte nach dem oben besprochenen Schema aus.
Versuche herauszufinden:
Sind die gelben oder die grünen Zonen maximale Auslenkung nach oben?
(Tipp: klicke in das laufende Programm, es zeigt die die Zeiger und ihre Überlagerung am jeweiligen Ort.)

Grüninger, Landesbildungsserver

[ Startseite Interferenzvorgang ]