Interferenzen auf der Mittelsenkrechten.

Interferenz auf der Mittelsenkrechten

Von zwei Erregern E1 (rot) und Erreger E2 (blau), die mit gleicher Frequenz und und gleichphasig schwingen (kohärent), gehen Wellen aus.

Zuerst wenden wir uns den Verhältnissen auf der Mittelsenkrechten zu.

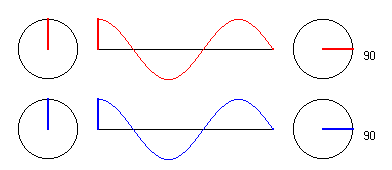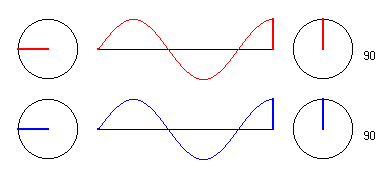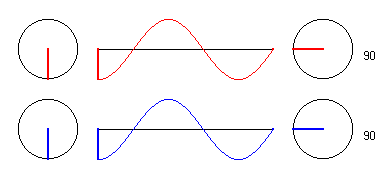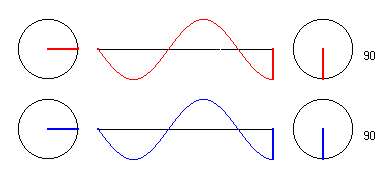
1.) Punkt in der Entfernung λ von den Erregern.

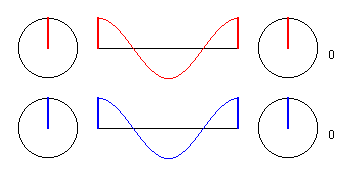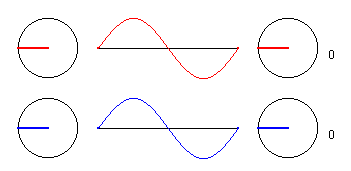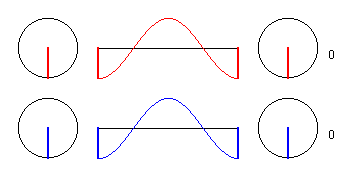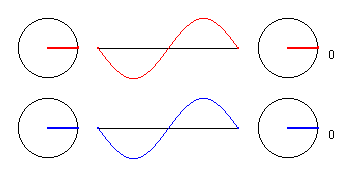
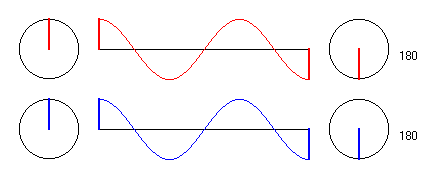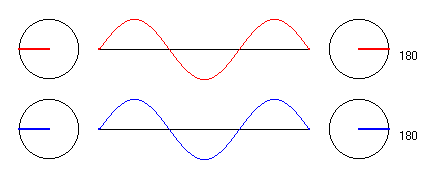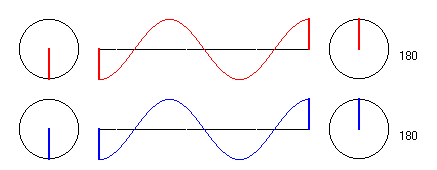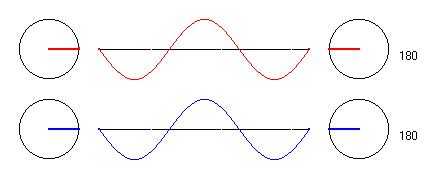
Wir betrachten zunächst einen Punkt P auf der Mittelsenkrechten, der von jedem der beiden Erreger gerade in der Entfernung λliegt. E1 zwingt also dem Teilchen in P eine Schwingung auf, die gleichphasig mit ihm ist (rote Schwingung). Dasselbe gilt für die von Erreger E2 ausgehende Schwingung (blaue Schwingung). Beide Schwingungen überlagern sich in P konstruktiv, so daß das Teilchen in Phase mit den Erregern, aber mit der doppelten Amplitude der Einzelschwingungen schwingt.

Alle Zeige rotieren "im Gleichtakt".
Die Gradzahlen ganz rechts sind die Phasenwinkel gegenüber dem jeweiligen Erreger, nicht die aktuellen Phasenwinkel zum jeweiligen Zeitpunkt.

Phasenbezug

Dieselbe Überlegung kann man auch für einen anderen Punkt anstellen, der in 2 * λ Entfernung von den Erregern liegt.(und für alle anderen Entfernungen mit n * λ)

2.) Punkt in der Entfernung 3/2 * λ.

Was ist anders, wenn sich der Punkt in der Entfernung 1,5 * λ befindet?
(allgemein (2k-1) * λ/2)

Nun, dann erzwingt der Erreger E1 eine Schwingung in Gegenphase zu der des Punktes, ebenso der Erreger E2. Insgesamt schwingt das Teilchen P wieder mit der doppelten Amplitude aber in Gegenphase zu den Errregern. Die Phasenverschiebung zu den Erregern ist hier also 180 Grad, aber die Zeiger der Teil- und der Gesamtamplitude des Teilchens im Punkt P sind wieder "im Gleichtakt".

In Gegenphase

3.) Ein allgemeiner Punkt auf der Mittelachse.

Hier ist noch eine Darstellung für einen Punkt P, der sich gerade in der Entfernung 1,25 * λbefindet. Hier ist Auslenkung des Teilchens P immer genau dann 0, wenn die Erreger maximal ausgelenkt sind, die Phasenverschiebung ist hier also 90 Grad. Wieder überlagern sich die beiden Einzelamplituden der Wellen von E1 und E2 konstruktiv zur Gesamtamplitude.

Allgemeiner Punkt auf der Mittelachse

4.) Die Gemeinsamkeiten.

Was ist also allen Punkten auf der Mittelachse gemeinsam?

  • Der Weg der Welle von E1 nach P ist immer genauso weit wie der Weg der anderen Welle von E2 zum Punkt P.
    Man sagt, der Gangunterschied der beiden Wellen ist 0.

  • das Teilchen im Punkt P schwingt zwar im Allgemeinen nicht phasengleich mit den Erregern E1 und E2, jedoch überlagern sich die von E1 und E2 ausgehenden Wellen auf der Mittelsenkrechte immer konstruktiv, der Phasenunterschied der beiden Wellen ist 0.

  • auf der Mittelsenkrechte ergibt sich also an allen Punkten eine maximale Schwankung der Amplitude.
    Hier ist es also immer hell (optische Interferenz), oder laut (Toninterferenz).
    Dies ist auch unabhängig von der Frequenz mit der die Erreger schwingen.

Grüninger, Landesbildungsserver

[ Startseite Interferenzvorgang ] [ zur nächsten Seite ]