Stehende Schallwellen mit zwei Randbedingungen:
kundtsches Rohr - zwei freie Enden.
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. |
Eine Plexiglasröhre ist an beiden Seiten offen. In der Röhre
befindet sich Korkmehl. |
Wie kommt es zu diesen Korkmehlwirbeln?
Vom Lautsprecher geht eine Schallwelle in das Rohr hinein (nach rechts).
Die Schallwelle wird auch an einem offenen Ende reflektiert. |
Warum gibt es die Wirbel nur bei ganz bestimmten Frequenzen?
Beim kundtschen Rohr wird die rücklaufende Welle durch das Rohr "zurückgeleitet" und gelangt wieder zum Lautsprecher. Einlaufende und reflektierte Welle haben dabei nahezu gleiche Intensität. Die rücklaufende Welle wird nun am Lautsprecher (ebenfalls ein offenes
Ende) nochmals ohne Phasensprung reflektiert und läuft wiederum nach
rechts in das Rohr zurück. Dabei überlagert sie sich aber nun mit der
Welle, die der Lautsprecher in diesem Augenblick abstahlt. |
Für welche Wellenlängen gibt es eine stehende Welle?
| Am linken Ende (Lautsprecher) ist immer ein
Schwingungsbauch, weil die Lautsprechermembran die Luftmoleküle
stets in kräftige (horizontale) Schwingung versetzt. Am rechten offenen Ende ist ebenfalls immer ein Schwingungsbauch. Die Luftmoleküle können sich dort horizontal bewegen. Man erkennt dies deutlich: An beiden Enden des Rohres rieseln Korkmehlteilchen aus dem Rohr (vgl. Film). |
Dazwischen können weitere Knotenstellen liegen, wobei zwei Knotenstellen immer einen Abstand von λ / 2 haben. Damit sind z.B. die Schwingungen möglich, die man in der folgenden Darstellung findet:
| Skizze | Bedingung | Bezeichnung |
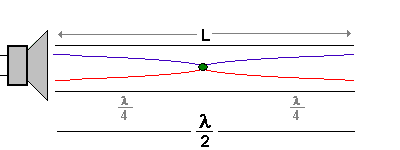 |
L = 1 * λ / 2 (1 Knoten) |
Grundschwingung oder 1. Harmonische |
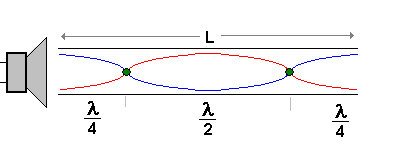 |
L = 2 * λ / 2 (2 Knoten) |
1. Oberschwingung oder 2. Harmonische |
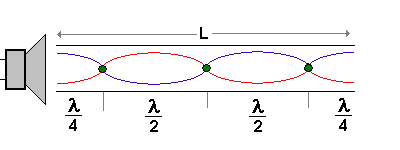 |
L = 3 * λ / 2 (3 Knoten) |
2. Oberschwingung oder 3. Harmonische |
| Es ergibt sich immer dann eine stehende Welle im kundtschen Rohr wenn
gilt: (Wobei k die Zahl der Knoten bzw. die Nummer der Harmonischen ist ) |
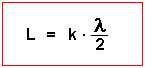 |
Probiere das in dem Applet aus, die schwarzen springenden
Punkte sind die Korkmehlteilchen.
Ein wenig rechnen muss Du allerdings schon noch ;-).
Es gilt c = f * λ
Fragen und Aufgaben:
Die Ausbreitungsgeschwindigkeit des Schalls in Luft wird mit 340 m/s angenommen. Die Rohrlänge ist 100 cm.
- Wie groß ist dann die Wellenlänge λ bei einer Frequenz von 170 Hz ?
- Zeige, dass sich dann bei 1,00 m Rohrlänge gerade die Grundfrequenz (1. Harmonische) ergibt.
Überlege nun, bei welchen Frequenzen sich die 2. und 3. Harmonische einstellen müssen.
- Prüfe mit dem Applet nach, indem Du die richtige Anregungsfrequenz eingibst und "Reset" klickst.
Ändere die Rohrlänge auf 50 cm.
- Bei welcher Frequenz stellt sich nun die Grundschwingung ein?
- Bei welchen Frequenzen erhält man die 2. Harmonische?
Langes Rohr, tiefer Ton - kurzes Rohr, hoher Ton.
Das kundtsche Rohr ist Grundlage für jede Art von Blasinstrumenten
(z.B. Flöte, Saxofon, Posaune) aber auch für die Orgel.
Beim Abdecken der Löcher, z.B. bei einer Flöte, wird der Ton tiefer,
weil sich die wirksame Rohrlänge vergrößert.
Auch bei der Orgel entscheidet die Rohrlänge über den gespielten Ton:
die langen Orgelpfeilen erzeugen die tiefen Töne, die kurzen die hohen
Töne.
| Orgelpfeifen berechnet: Wie lange müssen die Orgelpfeifen für folgende Töne sein?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
In der Praxis der Orgelbauer ist es allerdings ein wenig komplizierter, denn
eine Orgelpfeile ist kein einfaches kundtsches Rohr!
Wer mehr dazu wissen möchte, findet z.B.
![]() auf dieser Seite bei Wikipedia Antworten.
auf dieser Seite bei Wikipedia Antworten.
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (kundt_offen.zip) herunterladen und
in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : kundt_offen.zip ALT="gepackte Datei" BORDER="0" TITLE="gepackte Datei"> |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
|


