Gedämpfte Schwingungen.

Normalerweise sind Schwingungen keine freien Schwingungen, wie sie auf dieser Seite betrachtet wurden, sondern Schwingungen sind im Allgemeinen gedämpft, d.h. das schwingende System hat Energieverluste durch Reibung. Dem schwingenden System geht daher stets ein wenig seiner Energie verloren, die Amplitude der Schwingung nimmt ab.

Hier wird ein Modell betrachtet, bei dem die Reibungskraft proportional zur Geschwindigkeit des schwingenden Körpers ist. Dies ist bei vielen schwingenden System der Fall.

Die Lösung ist deutlich komplizierter als die die freien Schwingung. In der Schule wird sie meist deshalb nicht in aller Strenge behandelt, weil die Exponentialfunktion (exp) erst spät im Mathematikunterricht behandelt wird.

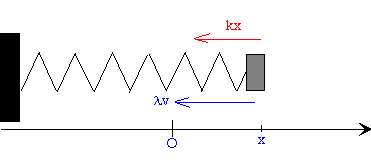
Um die Dämpfung zu beschreiben, nehmen wir an, dass zusätzlich zur Kraft der Feder F=-kx, die der Auslenkung x proportional und entgegengesetzt ist, nun noch eine zweite Kraft F_r=-lv wirkt, die von der Geschwindigkeit abhängt, dabei ist l eine Konstante, die von der jeweiligen Art des Schwingungssystems abhängt.

Die Bewegungsgleichung kann man also schreiben als

Schreiben wir wieder die Bewegungsgleichung in der Form einer Differenzialgleichung und berücksichtigen wir dabei, dass die Beschleunigung die zweite Ableitung der Auslenkung x und die Geschwindigkeit die erste Ableitung der Auslenkung x ist.

Die Lösung dieser Differenzialgleichung hat folgende Form:

Die wichtigsten Eigenschaften einer solchen gedämpften Schwingung sind folgende:

• die Schwingungsamplitude nimmt exponentiell mit der Zeit ab (Faktor exp(.)).
• die Energie des schwingungsfähigen Systems nimmt ebenfalls ab. Es muß Reibungsarbeit mit Kraft F_rverrichtet werden.
• im Phasenraum (v-x) beschreibt der schwingende Körper eine gedachte Bahn, die spiralförmig zum Koordinatenursprung geht.

Wenn die Dämpfung groß ist, dann kanng so groß wie w₀werden. Man nennt dies den aperiodischen Grenzfall. Dann kommen keine Schwingungen mehr zustande und die Auslenkung der Masse nähert sich allmählich der Gleichgewichtslage.

Aktivitäten.

Gib folgende Werte ein:

• die Auslenkung der Masse am Anfang x₀, in das Eingabefeld Posición
• die Anfangsgeschwindigeit der Masse v₀, in das Eingabefeld Velocidad.
• die Dämpfungskonstante g in das Eingabefeld Cte. amortiguamiento
• die Eigenfrequenz (Winkelgeschwindigkeit) des Systemsw₀=100 rad/s kann nicht verändert werden.

Drücke zu Start den Knopf Empieza.

Probiere folgende Dämpfungswerte g aus: 5 (leicht gedämpft), 50 (stärker gedämpft), 100 (aperiodischer Grenzfall), 110 (noch stärker gedämpft).

• beobachte die Auslenkung der Masse zu verschiedenen Zeitpunkten und das x-t- Diagramm.
• die gedachte Umlaufkurve im Phasenraum v-x, oben rechts.
• die Gesamtenergie als Funktion der Zeit E-t, unten rechts.

Man kann die Darstellung mit Pausa unterbrechen und mit Continua fortsetzen sowie mit Paso im Einzelschrittmodus weiterschalten.

Diese Seite ist eine verkürzte deutsche Schulversion dieser spanischen Originalseite .
Die Verwendung des Applets erfolgt mit freundlicher Genehmigung des Autors.