Die Elongationsenergie - was ist das?
Zwei Lösungsstrategien für mechanische Aufgaben.
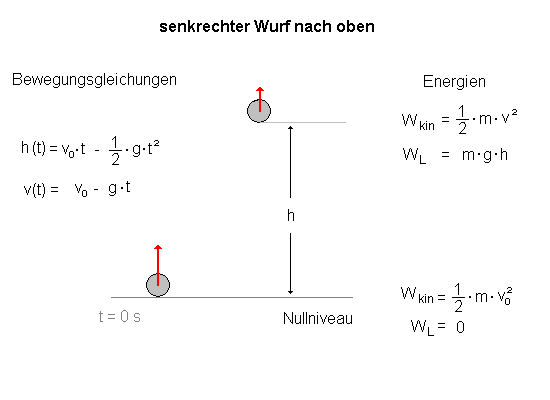
In der fortgeschrittenen Mechanik (z.Zt. in Baden-Württemberg meist in Klasse 10 des Gymnasiums) hast du gelernt, dass man Vorgänge wie z.B. den senkrechten Wurf nach oben oder auch die Bewegung an der schiefen Ebene prinzipiell auf zwei Arten beschreiben kann:
Immer führen beide Wege zum Ziel. Dabei ist aber der Weg
über die Energieerhaltung meist einfacher und schneller. |
 |
Gibt es auch bei den Schwingungen einen einfachen Lösungsweg über die Energieerhaltung?
Möchte man z.B. bei einem Feder-Masse-Pendel die Geschwindigkeit in einem beliebigen Punkt der Schwingung bestimmen, so ist dies nicht ganz einfach:
- man muss zunächst die Schwingungsgleichungen (unter Berücksichtigung der Anfangsbedingungen) aufstellen,
- danach mit der Weg-Zeit-Gleichung berechnen, wann die Masse diesen Punkt erreicht,
- und zuletzt diese Zeit in die Geschwindigkeits-Zeit-Gleichung einsetzen.
Die Zeit dient dabei nur als Zwischengröße - eigentlich
ist es uns egal, wann die Masse dort ist.
Geht das nicht auch einfacher und eleganter? - Doch, mit Hilfe der
Elongationsenergie!
Dazu müssen wir uns aber zunächst einmal erarbeiten, was das
eigentlich ist, dann wird gezeigt, dass dieses Prinzip auch für andere
Schwinger, z.B. den Wagen zwischen zwei Federn gilt. Schließlich gibt es
dann noch einen Vergleich zweier Lösungen mit Schwingungsgleichung und
Elongationsenergie für eine konkrete Aufgabe.
Herleitung der Elongationsenergie
beim Feder-Masse-Pendel.
Vertiefung der Elongationsenergie
beim Feder-Masse-Pendel.
Elongationsenergie
bei Wagen zwischen zwei Federn
Vergleich zweier
Lösungswege, eine Beispielaufgabe
Klaus-Dieter Grüninger, Landesbildungsserver, 2014