Herleitung der Elongationsenergie beim Feder-Masse Pendel.

1) Die Auslenkung in besonderen Punkten der Schwingung.

ausgewählte Verlängerungen bei einer Feder

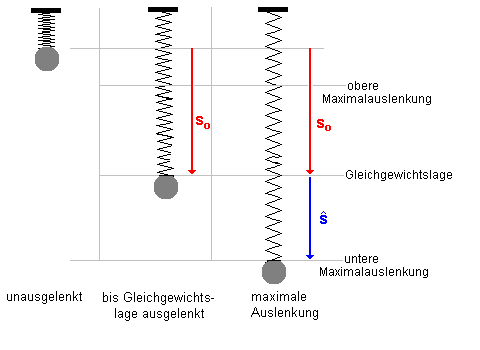Das linke Bild zeigt die Feder ohne Belastung (unausgelenkt).

Im mittleren Bild ist die Feder bis zur Gleichgewichtslage verlängert. Bei dieser Verängerung s_o ist die Federkraft F = D*s_o (nach oben) gleich groß wie die Gewichtskraft der Masse Fg = m*g (nach unten).

Aus dieser Gleichgewichtslage wird die Feder nun um eine zusätzliche Strecke s-Dach nach unten verlängert und die Masse von dort losgelassen.

2) Veränderung der Energieanteile zu Beginn der Schwingung.

Die untere Maximalauslenkung entspricht gleichzeitig dem Energie-Nullniveau, denn tiefer geht es nicht!

Wir betrachten die Energien in den Punkten 1 bis 6.

Wie verändern sich die verschiedenen Energieformen im ersten Teil der Schwingung?
Wir geben ihre Werte mitHilfe von Formeln entweder genau an, wenn dies möglich ist. Falls dies nicht möglich ist sagen wir wenigstens, ob sie sich gegenüber der Lage davor vergrößert oder verkleinert haben.

Punkt	Spannenergie	Lageenergie	Bewegungsenergie
0	maximal	0	0
1	nimmt ab	nimmt zu	nimmt zu
2			maximaleGeschwindigkeit
3	nimmt ab	noch größer	nimmt ab
4	minimal	maximal	0
5	nimmt zu (wie bei 3))	kleiner (wie bei 3))	nimmt zu (wie bei 3))
6	wie bei 2)	wie bei 2)	wie bei 2)

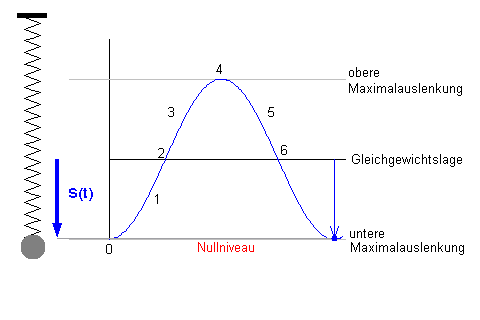3) Wie vergleichen die Gesamtenergien im Startpunkt (0) und in der Gleichgewichtslage (2).

Wir stellen die Energieformen im Startpunkt (0) und in der Gleichgewichtslage (2) zunächst zusammen.

Nun addieren wir die Energien in (0) und in (2) jeweils zur Gesamtenergie, multiplizieren die linke Seite aus und können dann noch an zwei Stellen vereinfachen:

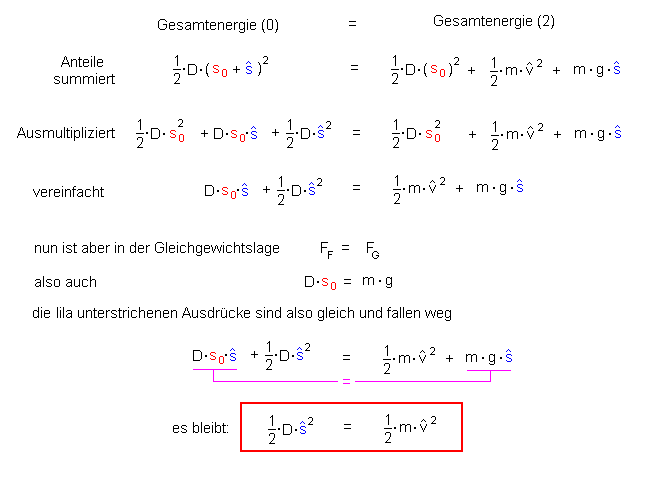
Was bedeutet diese Gleichung?

in der Gleichung kommt s_o gar nicht mehr vor, d.h. für die Geschwindigkeit der Masse in der Gleichgewichtslage v-Dach ist es völlig egal, wie weit die Feder bis zur Gleichgewichtslage ausgelenkt wurde!
Der Ausdruck 1/2*D*s_o² hat sich bei der Herleitung herausgekürzt. Das ist die Energie, welche die Feder bekommt, wenn die Masse darangehängt wird und sie bis zur Gleichgewichtslage verlängert wird. Diese Energie kommt letztlich aus der Gravitation.
entscheidend für v-Dach ist lediglich, wie weit die Masse aus der Gleichgewichtslage ausgelenkt oder verlängert wird. Verlängerung heißt mit einem Fremdwort "Elongation" (lat. elongare - engl. long) - also nennt man die Energie auch die Elongationsenergie.
Anschaulich ist die Elongationsenergie also die Spannenergie einer Feder, wobei die Verlängerung aber nicht auf die unausgelenkte Feder, sondern auf die Gleichgewichtslage bezogen wird.
die Elongationsenergie ist im Startpunkt (0) und im oberen Umkehrpunkt (4) gleich groß. Im einen Fall ist zwar s-Dach negativ (Position 0) und im anderen Fall positiv (Position 4), da s-Dach aber für die Elongationsenergie quadriert wird, spielt das Vorzeichen der Auslenkung keine Rolle.
In jeder anderen Auslenkung oberhalb und unterhalb der Gleichgewichtslage sind daher die Elongationsenergieen ebenfalls gleich groß. (z.B. + 5 cm und -5 cm bzw. +10 cm und -10 cm).
Ist die maximale Auslenkung s-Dach aus der Gleichgewichtslage groß, dann wird es auch die Geschwindigkeit in der Gleichgewichtslage v-Dach groß, sie sind zueinander proportional.

4) Viele Wege führen zum Ziel!

Du glaubst noch nicht so richtig, dass s_o wirklich keine Rolle spielt?

Nun, man kann auf diese Gleichung auch noch auf einem anderen Weg kommen.
Vielleicht überzeugt dich dieser Weg mehr!

Mit den Schwingungsgleichungen (unter Berücksichtigung der Anfangsbedingungen) hätten wir angesetzt:
Weg-Zeit-Funktion
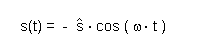
Die Geschwindigkeit v(t) ist dabei die Ableitung der s(t)-Funktion, also:
Geschwindigkeit: Ableitung der Weg-Zeit-Funktion
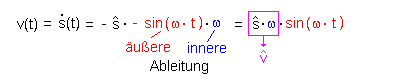
Fasst man zusammen, ergibt sich:

Die Lösung der Differentialgleichung 2. Ordnung ergibt für die Frequenz / Winkelgeschwindigkeit der Schwingung:

Quadriert und in (a) eingesetzt führt dies zu:
Omega eingesetzt
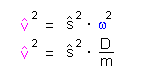
stellt man das noch etwas um und multipliziert beide Seiten mit 1/2 dann ergibt sich:
auch so kommt man auf Elongationsenergie!

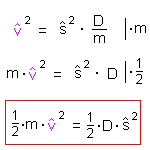
Das ist aber genau die Gleichung von oben, was das Prinzip der Elongationsenergie noch einmal zusätzlich bestätigt!

Vertiefung der Elongationsenergie beim Feder-Masse-Pendel.