Elongationsenergie beim Wagen zwischen zwei Federn.
Auf dieser Seite wird gezeigt, dass das Prinzip der Elongationsenergie nicht nur eine Eigenschaft des (senkrechten) Feder-Masse-Pendels darstellt, sondern sehr allgemeinerungsfähig ist. Wir betrachten den Wagen zwischen zwei (gleichen) Federn als Schwingungssystem.
1) Anfangssituation.
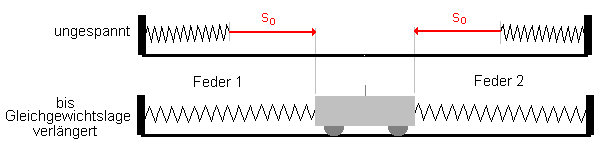
Die beiden - zunächst ungespannten - Federn werden am Wagen
eingehängt und dabei gespannt.
Wenn wir zwei gleiche Federn verwenden, werden beide dabei um die Strecke
s0 verlängert.
Da für die Energie die Spannungsrichtung keine Rolle spielt (bei der
Spannenergie wird s0 ja quadriert) muss der Experimentator hier
zunächst beim Spannen in beide Federn "Energie
hineinstecken".
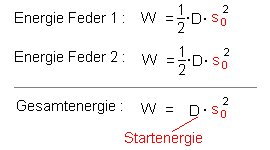
Dies ist:
2) Der Wagen wird ausgelenkt.
Nun wird der Wagen nach rechts ausgelenkt. Um es zeichnerisch einfach zu
machen, ist hier s-Dach gerade die halbe Wagenlänge, das gilt aber auch
allgemein, sofern s-Dach < s0 ist.
Der Wagen ist zunächst in Ruhe, also ist die Bewegungsenergie hier 0.
Lageenergie brauchen wir bei diesem Problem nicht zu berücksichtigen, denn
die Schwingung spielt sich ja immer in derselben Höhe ab.
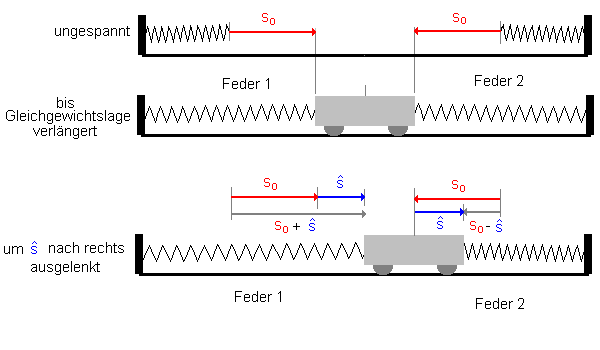
Beim Auslenken wird die Feder 1 (links) um die Strecke s-Dach länger, sie
hat nun also mehr Energie gespeichert, dafür verkürzt sich die Feder
2 (rechts) ebenfalls um s-Dach und hat nun weniger Energie gespeichert.
Was bedeutet das für die Gesamtenergie des Systems? Bleibt diese dabei
unverändert?
Schreiben wir es auf und multiplizieren aus:
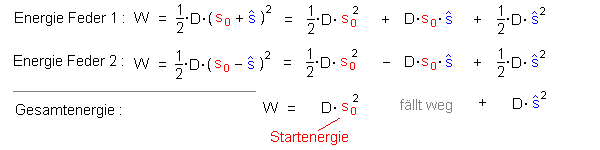
Addieren wir die beiden Federenergien zur Gesamtenergie, so
fällt das gemischte Glied (mittlerer Ausdruck) weg. |
Schreiben wir statt der Federhärten D auch hier die
Richtgröße D* - die Summe der beiden Federhärten, so folgt
für diese zusätzliche Energie beim Auslenken:
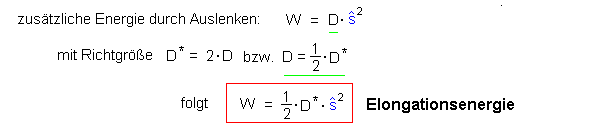
Die Energie hat also zugenommen und zwar nach der gleichen Formel
für die Elongationsenergie, die wir auch beim senkrechten
Feder-Masse-Pendel erhalten hatten!
Der einzige Unterschied ist, dass wir hier für D nicht die
Federhärten, sondern die Richtgröße D*, also die Summe der
Federhärten einsetzen müssen.
Wäre der Wagen nach links ausgelenkt worden, hätte sich dasselbe
ergeben, Feder 1 und Feder 2 hätten dabei einfach die Rollen getauscht.
3) Situation in der Gleichgewichtslage.
Der Wagen wird nun von rechts aus der ausgelenkten Position aus der Ruhe
losgelassen.
Welche Bewegungsenergie und welche Geschwindigkeit v-Dach hat er in der
Gleichgewichtslage?
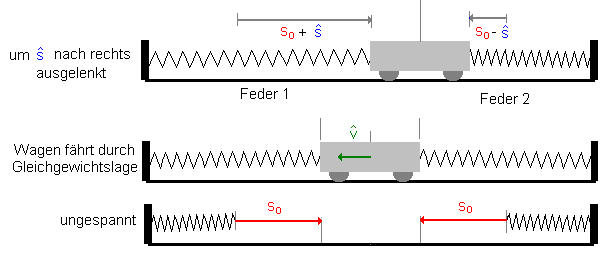
In der
Gleichgewichtslage bewegt sich der Wagen mit maximaler Geschwindigkeit und
damit maximaler Bewegungsenergie nach links. Aber auch die beiden Federn sind
immer noch um s0 gespannt.
Machen wir wieder die Energiebilanz:
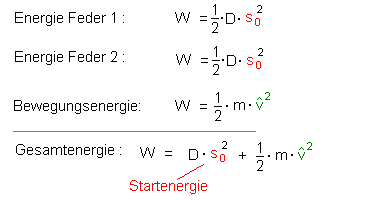
wieder steht links die Startenergie, die wir nicht berücksichtigen
müssen (s.o.).
Vergleichen wir also die Elongationsenergie in der maximalen Auslenkung rechts
und die Bewegungsenergie in der Gleichgewichtslage so gilt:
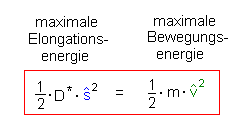
4) .. und wie ist das dazwischen? - Eine Beispielaufgabe.
Was können wir mit der Elongationsenergie nun anfangen?
Wir können damit z.B. eine Aufgabe, die mit den Schwingungsgleichungen
schwierig zu lösen wäre, recht einfach bewältigen:
Aufgabe:
Ein Wagen der Masse m = 500 g ist zwischen zwei gleichen
Federn der Federhärte D = 10 N/m eingespannt. Er wird um 20 cm
nach rechts ausgelenkt und von dort aus der Ruhe losgelassen.
Welche Bewegungsenergie und welche Geschwindigkeit hat er auf halber Strecke,
d.h. bei 10 cm Auslenkung?
Lösung:
Anfängliche Elongationsenergie nach Auslenken:
WStart = 1/2 * D-Stern * (s-Dach)2 =
1/2 * 20 N/m * (0,2 m)2 = 0,4 J.
Wenn der Wagen nur noch 10 cm ausgelenkt ist, dann ist die
Elongationsenergie kleiner, dafür steckt nun ein Teil der Anfangsenergie
in der Bewegung.
Für die Elongationsenergie bei Auslenkung 10 cm gilt:
Wel = 1/2 * D-Stern * (s)2 = 1/2 *
20 N/m * (0,1m)2 = 0,1 J.
Bei halber Auslenkung ist die Elongationsenergie nicht etwa auch halb so
groß, sondern nur 1/4, dies liegt an der Quadrierung!
In der Bewegung stecken also an dieser Stelle WStart -
Wel = 0,4 J - 0,1 J = 0,3 J, also 3/4 der
Anfangsenergie.
Mit W = 1/2 * m * v2 folgt daraus nach Auflösen nach
v das Ergebnis 1,09 m/s.
Erweiterung:
Bestimmt findest du mit der Elongationsenergie und dem Energieerhaltungssatz
auch heraus, an welcher Stelle Elongationsenergie und Bewegungsenergie gleich
groß sind!
Wie schnell ist der Wagen dort?
(Ergebnisse: s = 14,1 cm , v = 0,89 m/s)


