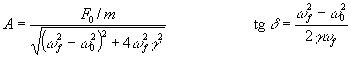Erzwungene Schwingungen im stationären Zustand.
|
Wie auf dieser Seite
dargestellt nimmt die Amplitude einer Schwingungen exponentiell
mit der Zeit ab, d.h. nach einer theoretisch unendlich langen Zeit,
befindet sich der schwingende Körper in der
Nulllage.(Gleichgewichtslage). Beschreibung.
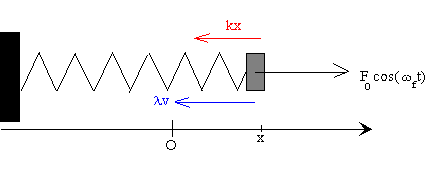
Es sei F0·cos(wf t) die anregende Kraft, die mit der Winkelgeschwindigkeit wf auf das schwingungsfähige System einwirkt. Die Bewegungsgleichung des gedämpft schwingenden Körpers ist daher:
Wenn man die Bewegungsgleichung in Form einer Differenzialgleichung angibt, folgt:
Die Lösung dieser Differnzialgleichung ist recht schwierig und
wird in der Schule nicht behandelt. Eine Teillösung der Differenzialgleichung ist:
Wobei die Werte für die Amplitude A und den Phasenwinkel d folgende Form haben
Man sieht, dass beide Faktoren von der Differenz der beiden Frequenzen abhängen.
Das Hauptmerkmal des Gleichgewichtszustand ist, dass die Geschwindigkeit der schwingenden Masse in Phase ( d = 0) mit der anregenden Kraft ist, wenn die Anregungsfrequenz wf gleich der Eigenfrequenz w0 des schwingungsfähigen Systems ist. Die anregende Kraft F und Auslenkung s sind dann also um 90 Grad phasenverschoben, d.h. bei maximaler Auslenkung ist die anregende Kraft minimal. Aktivitäten.Gib folgende Größen ein:
Drücke den Knopf Empieza. Im linken Teil des Applets sieht man die erzwungene Schwingung, die sich durch die Einwirkung der äußeren Kraft, die sich mit der Winkelgeschwindigkeit wf verändert, ergibt. Im rechten Teil des Applets kann man sich orientieren, wie die
Anregungsfrequenz relativ zur Eigenfrequenz des Systems liegt. Mit Pausa kann man die Darstellung unterbrechen, mit Continua fortsetzen. Paso schaltet im Einzelschritt-Modus weiter.
|
|||
Aufgaben:
- beobachte zunächst die Schwingung bei den voreingestellten
werden.
- gib als Anregungsfrequenz 100 ein.
Beobachte, dass Geschwindigkeit und anregende Kraft nun in der Resonanz in Phase sind.
Beide werden bei maximaler Auslenkung minimal und im Nulldurchgang maximal.
Schalte dazu die Darstellung im Einzelbildmodus weiter.
- verändere die Dämpfung.
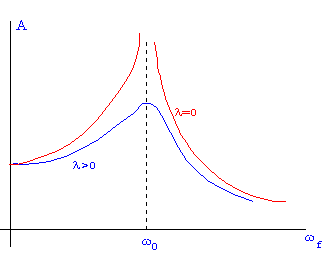
Wie verändern sich die Amplitude und die beiden Kurven rechts, wenn man die Dämpfung verändert?
- warum gibt das Programm nichts aus, wenn man als Anregungsfrequenz
100 und als Dämpfung 0 eingibt?
Was geschieht bei geringer Dämpfung (1) und bei großer Dämpfung (> 30)?
Diese Seite ist eine deutsche Schulversion
dieser
spanischen Originalseite.
Die Benutzung des Applets erfolgt mit freundlicher Genehmigung des Autors.