Die Schwingfigur - ein Feder-Masse-Pendel.
 |
Eine Holzfigur an einer Feder ist ein beliebtes Spielzeug. Man kann es
in Geschenk- oder Spielwarengeschäften kaufen, oder man wird auch im
Internet unter den Begriffen "Schwingfigur" oder "Jumper"
fündig. Dabei liegen die Kosten pro Figur teilweise deutlich unter 10
Euro. Hier sind einige Bezugsmöglichkeiten: http://www.creativbay.de/Schwingfiguren---43.html http://www.volkskunstshop.com/holzspielzeug-schwingfiguren-c-248_428.html Physikalisch betrachtet handelt es sich dabei um ein Feder-Masse-Pendel. Man kann die Figur als Einstieg in das Thema verwenden und daran die Theorie des Feder-Masse-Pendels im Unterricht erarbeiten. Auf Grund des günstigen Preises eignen sich diese Figuren aber auch für ein Praktikum zu diesem Thema in mehreren Gruppen. Messlatten, Waagen und Stoppuhren dürften üblicherweise in genügender Stückzahl vorhanden sein. |
1.) Behandlung in einem Praktikum.
Ein Arbeitsblatt zu einem Praktikum können Sie
hier
herunterladen ![]()
In einer Doppelstunde wiederholten die Schülerinnen und Schüler zunächst die Herleitungen aus dem Unterricht und boten die Ergebnisse in einem Kurzvortrag dar. Danach wurde die Masse m der Holzfigur ermittelt und damit die Federhärte D bestimmt (D = (m * g) / so). Dabei muss von der Länge der Feder in der Gleichgewichtslage natürlich noch die Grundlänge der Feder abgezogen werden. Anschließend kann man die Periodendauer nach der Schwingungsgleichung berechnen und danach das Ergebnis im Experiment überprüfen.
Einige weiterführende Aufgaben könnten sich anschließen (Punkt 3), die man aber auch als Hausaufgabe bearbeiten kann.
2.) Das Problem als virtuelles Experiment.
Aufgabe: Bestimme Masse m, Periodendauer T und Federhärte D mit Hilfe von Foto und Film.
|
 |
|
Die Schwingfigur wird aus der Gleichgewichtslage nach unten ausgelenkt und
losgelassen.
Dies gelingt besonders gut, wenn Du den Film (in größerem Format) hier herunterlädst Nimm als Bezugspunkt z.B. die rote Zunge oder die schwarze Nase des Hundes. Die Filmaufnahme erfolgte mit 30 Bilder pro Sekunde.
|
3.) Ein kniffliges Problem.
Folgende Frage (Frage e auf dem Arbeitsblatt) ist interessant:
| Kann man die Masse m der Figur und die Federhärte D nur mit Hilfe
einer Messlatte und einer Stoppuhr bestimmen? Falls ja, wie? Falls nein, warum nicht? |
Für die Federhärte D und die Periodendauer der Schwingung T gelten folgende Gleichungen:
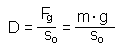 |
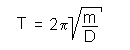 |
Misst man also die Periodendauer T und die Verlängerung bis zur Gleichgewichtslage so, so würde man erwarten, dass sich die zwei Unbekannten - die Masse m und die Federhärte D - aus den zwei Gleichungen bestimmen lassen.
Dies gelingt aber nicht!
Substituiert man die Masse m (links) oder die Federhärte D (rechts), dann kürzt sich die jeweils andere Größe weg!
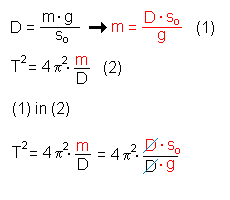 |
bzw. | 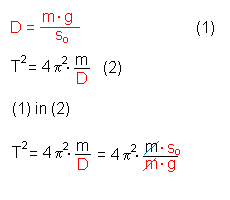 |
| In beiden Fällen bekommt man:
|
||
Um Missverständnisse zu vermeiden: so ist die
Verlängerung der Feder bis zur
Gleichgewichtslage, und hat natürlich nichts mit der Auslenkung
aus der Gleichgewichtslage ^s zu tun! Die Periodendauer
hängt von dieser Auslenkung ja nicht ab!
Man kann, wenn man so und T experimentell bestimmt, zwar zeigen,
dass die Gleichung stimmt, jedoch gelingt es auf diese Weise nicht, die Masse m
und die Federhärte D getrennt zu bestimmen.
Man bekommt über beide Gleichungen immer nur den Quotienten m/D
bzw. D/m heraus!
Dieses Problem hat seine Parallele in der Bewegung von
geladenen Teilchen in Feldern. Auch dort gelingt es nur die
spezifische Ladung, also den Quotienten e/m,
zu bestimmen.
Die Elementarladung e und die Masse m - z.B. eines Elektrons - lassen sich
nicht ohne weitere Messungen getrennt bestimmen.
Im Millikan-Experiment
benötigt man als zweites unabhängiges Experiment den Sinkversuch des
Öltröpfchens. Auf diese Weise lässt sich seine Masse bestimmen
und daraus kann man die Ladung des Tröpfchens (bekanntlich ein Vielfaches
der Elementarladung) ermitteln.
Auch beim Feder-Masse-Pendel muss die Masse des Pendelkörpers getrennt
bestimmt werden.
4.) Noch ein Problem zum Nachdenken .....
Ein anderer Hersteller von Schwingfiguren möchte eine Schwingfigur bauen, die gerade die doppelte Periodendauer hat.
|
Mögliche Lösung:
Bei einer Masse von 90 g und einer Federhärte von 2,2 N/m ist die
Verlängerung der Feder etwa 40 cm.
Die erste Möglichkeit die Periodendauer zu verdoppeln besteht
darin, an die gleiche Feder ein Spielzeugtier vierfacher Masse zu
hängen. Bei einer Masse von fast 400 g ist die Verletzungsgefahr doch
schon ganz erheblich und die Figur wird teurer. Außerdem wird die Feder
dann in der Gleichgewichtslage immerhin um 1,6 m verlängert.
Die zweite Möglichkeit wäre die Masse beizubehalten, aber
eine Feder zu verwenden, die nur 1/4 der Federhärte hat. Wieder
wäre die Verlängerung der Feder (so = F / D)
stolze 1,6 m. Diese Feder ist nun aber sehr empfindlich, die
Wahrscheinlichkeit, dass sie beim Spiel schnell kaputt geht, ist
groß.
Bleibt noch als dritte Möglichkeit die Masse zu verdoppeln
und die Federhärte zu halbieren.
Auch diesmal ist die Verlängerung der Feder bis zur Gleichgewichtslage 1,6
m, daran ändert sich bei keiner der Lösungen etwas!
Das ist nach der Gleichung
![]() von oben auch
klar: Eine Vergrößerung der Periodendauer geht nur über ein
größeres so, alle anderen Größen liegen fest.
Immerhin wäre hier die Verletzungs- und Zerstörungsgefahr etwas
kleiner.
von oben auch
klar: Eine Vergrößerung der Periodendauer geht nur über ein
größeres so, alle anderen Größen liegen fest.
Immerhin wäre hier die Verletzungs- und Zerstörungsgefahr etwas
kleiner.
Wahrscheinlich würde man aber zu dem Schluss kommen, dem Hersteller zu
raten, seine Pläne aufzugeben ;-)
Fazit: Man sieht, das auf den ersten Blick eigentlich recht langweilige Feder-Masse-Pendel bietet auch noch ganz interessante Aspekte und motivierende Zugänge.
Klaus-Dieter Grüninger, Landesbildungsserver, 2009


