Gedämpfte harmonische Schwingung und Kreisbewegung.

Mit diesem Java-Applet kann man die gedämpften Schwingung erforschen, so wie sie sich in der Wirklichkeit eigentlich immer ergibt:
Lenkt man ein Federpendel aus und lässt es los, so nimmt die Amplitude im Laufe der Zeit immer mehr ab, bis die Schwingung schließlich zum Erliegen kommt.
Dies liegt daran, dass der Pendelkörper beim Schwingungsvorgang ständig Luft verdrängen muss, es wird Reibungsarbeit verrichtet.
Auch an der Aufhängung entsteht Reibung. Diese Reibungsarbeit geht zu Lasten der Energie des Federpendels, die dadurch immer mehr abnimmt.

1.) Kurze Theorie der gedämpften Schwingung.

Eine ungedämpfteSchwingung kann mathematisch durch folgende Form dargestellt werden:

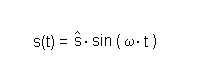
Dabei ist s-Dach die (konstante) Amplitude der Schwingung.

Wenn man noch eine andere Startbedingung (z.B. Federpendel startet vom oberen Umkehrpunkt aus) zulässt, dann kann man dies durch das Einfügen einer Phasenlage berücksichtigen.
Ist der Phasenwinkel δ z.B. 90° (oder im Bogenmaß π / 2), dann ist zum Zeitpunkt t = 0 s der erste Klammerausdruck (ω mal t) = 0. Ingesamt steht dann in der Klammer sin(90°) - und das ist 1. Die Amplitude zu Beginn des Schwingungsvorgangs ist dann gerade s-Dach.

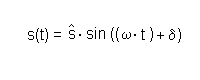
Bisher ist das die Gleichung für eine ungedämpfte Schwingung, bei der die Amplitude s-Dach unverändert bleibt.

Ist die Reibung von der Geschwindigkeit abhängig (was hier der Fall ist), dann nimmt die Amplitude im Laufe der Zeit exponentiell ab. Das Minuszeichen im Exponenten bedeutet "kleiner werden", die Abnahme erfolgt linear mit der Zeit. Wie schnell die Amplitude abnimmt, hängt vom Dämpfungsfaktor γ ab.
Für die gedämpfte Schwingung gilt dann:

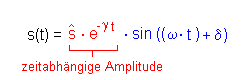
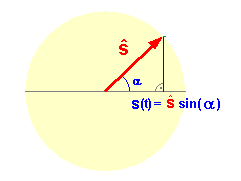
Ist die Kreisdarstellung aktiviert (Häkchen in Checkbox), sieht man, dass die Länge des rotierenden Pfeils (rot) kleiner wird. Seine Spitze bewegt sich also auf einer Spiralbahn in Richtung Mittelpunkt. Der rote Pfeil entspricht dem roten Teil der Gleichung (zeitabhängige Amplitude) Projiziert man diesen (roten) Pfeil auf die Vertikale, so bildet man den Sinus des Winkels sin(α(t)) = sin(ω*t)- multipliziert mit der Amplitude s-Dach. Die Länge des blauen Pfeils ist damit also die Amplitude zum jeweiligen Zeitpunkt s(t).

Wie stark die Reibung ist, kann man im Applet durch die Wahl der Dämpfung γ einstellen.
Wählt man hier "0", so ist die Schwingung ungedämpft und die Länge des roten Pfeils bleibt konstant, seine Spitze läuft in diesem Fall auf einem Kreis um.
Bei sehr starker Dämpfung (γ groß wählen), bekommt man u.U. den aperiodischen Grenzfall, d.h. die Amplitude nimmt so schnell ab, dass sich die Schwingung praktisch sofort an die Nulllinie annähert.

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (kreisundfederpendel_ged.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) © Javascript dieses Problems : Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg, 2009