Auf dieser Seite geht es um freie Schwingungen, die man z.B.bekommt, wenn eine Masse m an einer elastischen Feder der Federhärte k schwingt.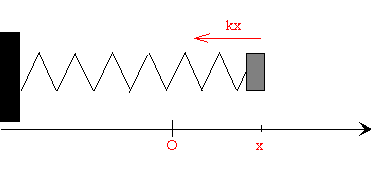

Wenn die Masse um eine Strecke x aus der Gleichgewichtslage ausgelenkt ist, wirkt auf sie eine Kraft, die proportional zur Auslenkung x ist und deren Richtung der Auslenkung entgegengesetzt ist, wie man in der Abbildung sieht.

Die Bewegungsgleichung kann man schreiben als:

Dabei ist -kx die Kraft der Feder (F=D*s, hier k*x), sie ist der Auslenkung x proportional, aber entgegengesetzt (daher das - Vorzeichen).
In der Zeichnung ist die Masse aus der Gleichgewichtslage (O) um die Strecke x nach rechts (positive x-Achse) ausgelenkt, die dazu proportionale Kraft der Feder wirkt aber nach links (in Richtung negativer x-Achse).
Diese Federkraft wirkt nach dem Kraftgesetz von Newton als beschleunigende Kraft (F=m*a).

Wenn man noch berücksichtigt, dass die Beschleuningung die zweite Ableitung der Auslenkung x ist, kann man diese Gleichung als Differenzialgleichung zweiter Ordnung schreiben.

In der Physik gibt es ganz verschiedene schwingungsfähige Systeme - in der Mechanik, in der Elektrizitätslehre und bei schwingenden Flüssigkeitssäulen - die man mit einer solchen Differenzialgleichung zweiter Ordnung beschreiben kann. Alle haben die gleiche Lösung: die harmonischen Funktionen Sinus und Cosinus.Vergleiche hierzu folgende Seite.

Die Lösung dieser Differenzalgleichung ist

Anfangsbedingungen

Die Lage x₀ und die Geschwindigkeit v₀ ganz zu Beginn der Schwingung bestimmen die Amplitude A und den Phasenwinkel j. Für t=0 ist

x₀=A·sinj
v₀=Aw₀·cosj

In diesen Gleichungssystemen hängen A und j also von den Werten von x₀ und v₀ ab.

Beispiel: Nehmen wir ein schwingungsfähiges System mit der Winkelgeschwindigkeit w₀=100 rad/s an. Wir wissen weiter, dass die Anfangsauslenkung des Teilchens x₀=5 beträgt und es aus der Ruhe, also mit v₀=0 startet. Dann können wir die Gleichungen schreiben als

5=A·sinj
0=100·A·cosj

Und die Gleichung des schwingungsfähigen Systems ist dann

x=5·sin(100t+ p/2)

(Abstraktere Ergänzung)

Eine andere Betrachtungsweise des schwingungsfähigen Systems wäre ein sogenannter Phasenraum, in dem der Impuls oder die Geschwindigkeit v auf der vertikalen Achse und die Auslenkung des schwingungsfähigen Körpers (also der Masse) auf der horizontalen Achse aufgetragen ist.

x=A·sin(w₀+ j)
v=A·w₀cos(w₀+ j)

Eliminiert man die Zeit t in diesen beiden Gleichungen, so bekommt man die Gleichung eines gedachten umlaufenden Punktes in diesem Phasenraum, es ist die Gleichung einer Ellipse.

Energie des schwingungsfähigen Systems.

Das Hauptmerkmal einer freien Schwingung ist, dass die Amplitude der Schwingung konstant bleibt und daher die Gesamtenergie des Systems konstant bleibt. Das System verliert also keine Energie. Die Gesamtenergie E ist also die Summe aus der Bewegungsenergie der Masse und der Spannungsenergie der Feder. Dies ist gleich der Spannungsenergie, die die Feder vor Beginn der Schwingung durch Spannen erhalten hat.

Aktivitäten.

Setze Werte für folgende Größen ein:

• die Ausleunkung am Anfang x₀, in das Eingabefeld Posición
• die Anfangsgeschwindigkeit des Körpers v₀, in das Eingabefeld Velocidad.
• die Winkelgeschwindigkeit von w₀=100 rad/s kann hier nicht verändert werden.

Drücke den Knopf Empieza.

• beobachte die Auslenkung der Masse zu verschiedenen Zeitpunkten und das x-t- Diagramm.
• die gedachte Umlaufkurve im Phasenraum v-x, oben rechts.
• die Gesamtenergie als Funktion der Zeit E-t, unten rechts.

Man kann die Darstellung mit Pausa unterbrechen und mit Continua fortsetzen sowie mit Paso im Einzelschrittmodus weiterschalten.

Probiere folgende Möglichkeiten aus:

• lasse die Geschwindigkeit (velocidad) auf 0 und gebe eine positive und eine negative Auslenkung ein. Von wo startet die Masse?
• setzte die Auslenkung auf 0 (die Masse startet also aus der Ruhelage) und gib eine Anfangsgeschwindigkeit ein.