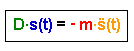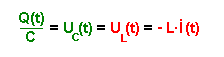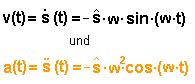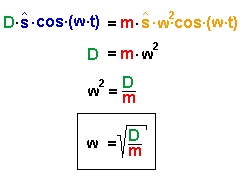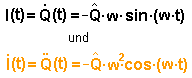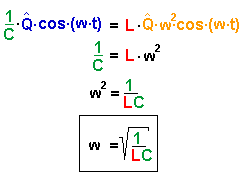Mechanische und elektrische Schwingungen - Vergleich der Schwingungsgleichungen-

Mechanische und elektrische Schwingungen
- ein Vergleich.

Vergleich der Schwingungsgleichungen:

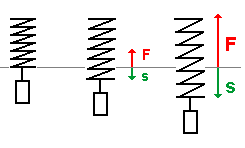
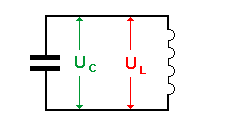
Die mechanischen Schwingungen eines Federpendels oder eines zwischen zwei Federn eingespannten Wagens haben sehr viel mit den elektrischen Schwingungen eines Schwingkreises aus Kondensator und Spule gemeinsam.

Mehr dazu hier.

Von statischen und dynamischen Energieformen:

Statische Energieform - Energiespeicher
Feder

ist ein Energiespeicher für Spannungsenergie
W=1/2 D s² 		Kondensator

Speichert Energie in seinem elektrischen Feld
(Energie der ruhenden Ladung)
W=1/2 C U²

kinetische oder dynamische Energieform - etwas bewegt sich.
Masse

nur wenn sich die Masse bewegt hat sie Bewegungs- oder kinetische Energie

W=1/2 m v²		 Spule

nur wenn die Spule stromdurchflossen ist, ist in ihrem Magnetfeld Energie gespeichert. Diese Energie ist also eine Folge der bewegten Ladungsträger
W=1/2 L I²

In beiden Fällen findet dabei ständig eine Umwandlung von einer statischen Energieform (Federspannung, Kondensatorladung) in eine kinetische Energieform (bewegte Masse, Strom in der Spule) statt.

Vergleich der mathematischen Lösungen der beiden Schwingungssysteme:

{short description of image} {short description of image}

Spannen einer Feder

  • Die Federkraft ist der Auslenkung s proportional aber entgegengesetzt.
  • Die Federkraft wirkt für die Masse als beschleunigende Kraft.
  • Die Beschleuningung weist also in Richtung von F .
  • Die Beschleunigung a ist zu s ebenfalls proportional und entgegengesetzt.

Kräftegleichung :

Für jeden Zeitpunkt gilt:
Kräftegleichung

Diese Gleichung gilt es nun zu lösen:
Momentanbeschleunigung

Die Gleichung ist also eine Differenzialgleichung 2. Ordnung
auf der einen Seite steht die Auslenkung s(t) auf der anderen Seite die zweite Ableitung davon, also kurz:
Differenzialgleichung

Laden eines Kondensators

  • Die Spannung Uc am Kondensator ist der Ladung Q proportional.
  • beide Spannungen - ULund damit UC - sind zu allen Zeiten gleich.
  • ist z.B. die Stromstärke I in der Spule maximal, dann ist ihre Änderung 0. In diesem Augenblick ist ULund damit UC also 0, der Kondensator ganz entladen.


Spannungsgleichung :

Für jeden Zeitpunkt gilt:
Spannungsgleichung

Diese Gleichung gilt es nun zu lösen:
Änderung der Momentanstromstärke

Die Gleichung ist also eine Differenzialgleichung 2. Ordnung
auf der einen Seite steht die Ladungsmenge Q(t)auf der anderen Seite die zweite Ableitung davon, also kurz:
Differenzialgleichung

Zum Zeitpunkt t=0 soll die Feder maximal gespannt sein.

Zum Zeitpunkt t=0 soll der Kondensator maximal geladen sein.

Lösungsansatz:
Lösungsansatz

die Ableitungen sind:
Ableitung

eingesetzt ergibt sich:
in DGL eingesetzt

Lösungsansatz:
Lösungsansatz

die Ableitungen sind:
Ableitung

eingesetzt ergibt sich:
in DGL eingesetzt

Man kann also sehr leicht von der einen Formel in die andere Formel umdenken, indem man einfach die Kenngrößen der statischen Elemente (Feder, Kondensator) und die der dynamischen Elemente (Masse, Spule) entsprechend ersetzt.

Wie man mit Hilfe eines Computers mit Soundkarte und eines Tonaufzeichnungs-Freeware-Programms den oben hergeleiteten Zusammenhang experimentell prüfen kann findet man hier