Feder-Masse-Schwinger
Feder und Masse

Elektrischer Schwingkreis
Kondensator und Spule

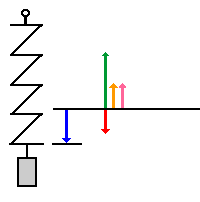
• Auslenkung s, Federkraft F_f, Kraft F_res und Beschleunigung a sind maximal.
  
  
• Die Geschwindigkeit der Masse ist 0.

Die Messinstumente haben den Nullpunkt in der Mittelstellung!

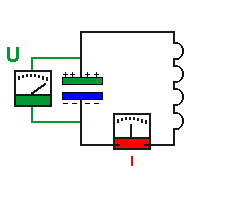
• Die Ladungsmenge Q auf den Kondensatorplatten und die Spannung am Kondensator sind maximal.
  
  
• Die Stromstärke I ist 0, die Elektronen ruhen also.

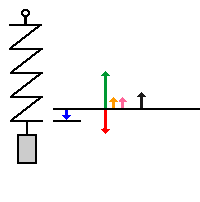
• Der Körper wird losgelassen.
  
  
• Die Feder entspannt sich (Auslenkung s, F_f und F_res und Beschleunigung a werden kleiner)
  
  
• Der Körper wird beschleunigt, seine Geschwindigkeit v nimmt zu .
  
  
• die kinetische Energie des Körpers (Masse) nimmt zu, die Spannungsenergie (Feder) nimmt ab.

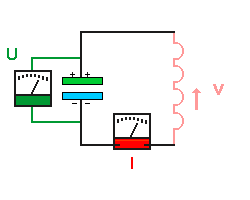
• Der Kondensator wird mit der Spule verbunden.
  
  
• Der Kondensator entlädt sich, Landung Q wird kleiner, die Spannung am Kondensator sinkt (Q=C*U).
  
  
• die Elektronen werden beschleunigt, d.h. die Elektronengeschwindigkeit v nimmt zu, die Stromstärke I in der Spule steigt.
  
  
• die Energie des Magnetfeldes (Spule) nimmt zu, die Energie des el. Feldes (Kondensator) nimmt ab.

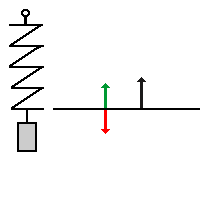
• Die Auslenkung aus der Ruhelage s, die F_res und die Beschleunigung a der Masse sind in diesem Augenblick 0.
  
  
• die Masse wird nun nicht mehr schneller, sie hat ihre maximale Geschwindigkeit erreicht.
  
  
• die gesamte Energie steckt in der Bewegung des Körpers.

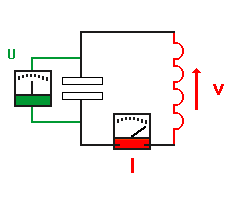
• Der Kondensator ist gerade ganz entladen, Q ist also gerade 0, damit ist auch die Spannung am Kondensator 0.
  
  
• die Elektronen werden nun nicht mehr schneller, sie haben ihre maximale Geschwindigkeit erreicht, die Stromstärke ist maximal.
  
  
• die gesamte Energie steckt im Magnetfeld der Spule.

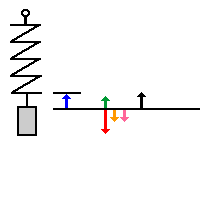
• Der Körper bleibt nicht stehen, er bewegt sich über die Gleichgewichtslage hinaus.(Trägheit der Masse)
  
  
• die Richtung der Geschwindigkeit bleibt erhalten
  
  
• der Körper wird nun abgebremst, seine Geschwindigkeit sinkt.
  
  
• die Feder wird in der umgekehrten Richtung gespannt.

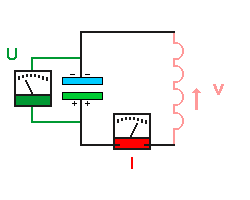
• Die Elektronen bleiben nicht stehen, sie bewegen sich in der gleichen Richtung weiter. Die Stromstärke bleibt also zunächst erhalten (lenz'sche Regel)
  
  
• die Richtung der Stromstärke bleibt erhalten.
  
  
• danach werden die Elektronen langsamer, die Stromstärke sinkt.
  
  
• der Kondensator wird entgegengesetzt geladen.

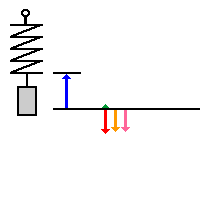
• der Körper ist maximal nach oben ausgelenkt.
• F_res und Beschleunigung a werden maximal
• der Köper kommt für einen Moment zur Ruhe (v=0) , ehe er nach unten beschleunigt wird.
• Die ganze Energie steckt wieder in der Spannung der Feder, die kinetische Energie der Masse ist 0.

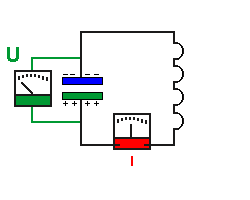
• der Kondensator ist wieder maximal geladen.
• die Elektronen sind zur Ruhe gekommen, die Stromstärke ist wieder 0
• die ganze Energie steckt wieder im elektrischen Feld des Kondensator, die Energie im Spulenfeld ist 0.

Der ganze Vorgang in zeitlicher Abfolge:

(Man kann in die Animation klicken und diese im Schrittmodus weiterschalten)

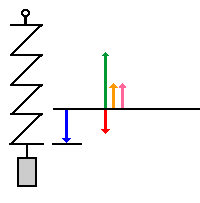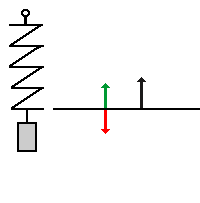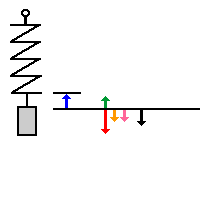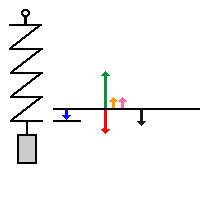
Auf folgende Dinge solltest du besonders achten:

• die Gewichtskraft F_g bleibt immer gleich. Die Federkraft ist um so größer je mehr die Feder gespannt ist.
  
  
• resultierende Kraft F_res und Beschleunigung a sind immer der Auslenkung s entgegengesetzt.
  
  
• die resultierende Kraft F_res ist der Auslenkung s proportional.
  
  
• ist die Auslenkung a maximal (max. Energie in der Feder) ist die Geschwindigkeit v=0.
  
  
• ist die Geschwindigkeit maximal ist die Auslenkung der Feder aus der Ruhelage gleich 0. (Maximale Energie in der Bewegung.

Der ganze Vorgang in zeitlicher Abfolge:

(Man kann in die Animation klicken und diese im Schrittmodus weiterschalten)

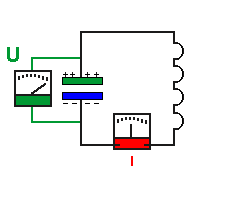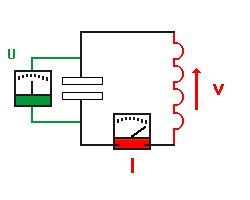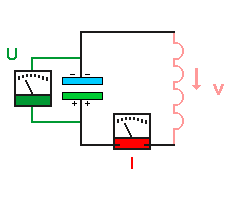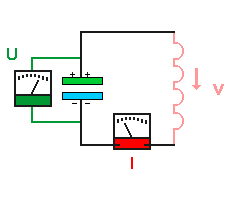
Auf folgende Dinge solltest du besonders achten:

• ist die Ladung Q auf dem Kondensator und damit die Spannung maximal, ist die Stromstärke also die Geschwidndigkeit der Elektronen gleich 0.
  
  
• ist die Stromstärke maximal, d.h. ist die Geschwindigkeit der Elektronen besonders groß, ist die Ladung auf dem Kondensator 0.