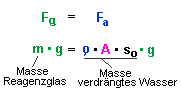Reagenzglas schwingt im wassergefüllten Standzylinder.
1.) Gleichgewichtslage :
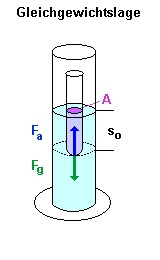 |
Ein Reagenzglas, das unten zur Stabilisierung beschwert ist, wird in
einen Standzylinder eingeführt. Das Reagenzglas verdrängt dabei ein
bestimmtes Volumen Wasser (in der Darstellung violett) und erfährt daher
eine Auftriebskraft Fa nach oben. |
| Der Einfacheit halber nehmen wir an, dass das Reagenzglas
unten nicht gewölbt, sondern eben ist, dass das Reagenzglas also eine
zylindrische Form hat. Im Gleichgewichtszustand gilt daher: |
|
2.) Zusätzliches Eintauchen :
 |
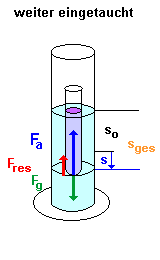 |
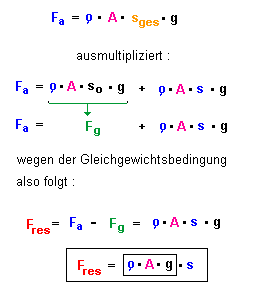
| Wird das Reagenzglas um eine zusätzliche Strecke s nach unten
gedrückt, verdrängt es nun mehr Wasser und die Auftriebskraft Fa (nach oben) wird
größer. Damit dies der Fall ist, müssen zwei Bedingungen erfüllt sein:
Die erste Bedingung ist sicher erfüllt, denn das Reagenzglas wird nach
unten gedrückt und die resultierende Kraft zeigt nach oben. Ist die zweite Bedingung auch erfüllt? Die Auftriebskraft Fa ist nun :
|
Da die Querschnittsfläche A, die Fallbeschleunigung g und die Dichte konstant sind, ist also die resultierende Kraft der Auslenkung s aus der Gleichgewichtslage proportional.
Die Richtgröße D ist damit:
![]()
Setzt man dies in die Lösung der Schwingungsgleichung ein so ergibt sich:
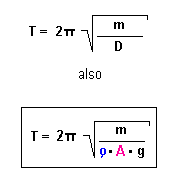
Möchte man also "langsame" Schwingungen haben, muß das Reagenzglas eine große Masse und eine kleine Querschnittsfläche A haben.
Zwischen diesem Problem und dem Federpendel gibt es viele Gemeinsamkeiten.
Klicken Sie für
einen Vergleich beider Systeme bitte hier.
Experimentell läßt sich die Frage, ob die Schwingung sinus- oder cosinusförmig ist, besonders elegant mit Hilfe der Videoanalyse klären. Klicken Sie dazu bitte hier.