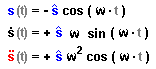Federpendel :

Reagenzglas :

Die Feder wird durch die angehängte Masse verlängert. Sie möchte sich wieder zusammenziehen. Es ergibt sich eine Federkraft F_f nach oben.

Das Reagenzglas verdrängt Wasser und erfährt dadurch die Auftriebskraft F_a nach oben, sie ist gleich der Gewichtskraft der verdrängten Flüssigkeitsmenge (Prinzip von Archimedes)

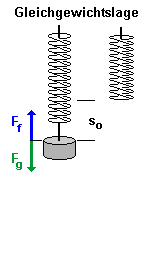
Die Feder wird so weit gespannt, bis die Federkraft F_f gleich groß wie die Gewichtskraft F_g der angehängten Masse ist.

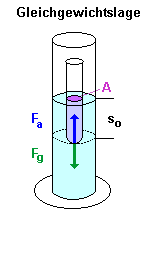
Das Reagenzglas taucht so weit ein, bis die Auftriebskraft F_a gleich groß wie die Gewichtskraft F_g des Reagenzglases ist.

Es gilt:

Es gilt:

Die rückstellende Federkraft ist der Verlängerung der Feder s_o proportional.

Die rückstellende Auftriebskraft ist der Eintauchtiefe s_o im Wasser proportional.

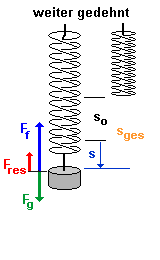
zusätzliche Auslenkung nach unten :

Wird die Feder weiter gespannt, so wird die Federkraft F_f größer als die Gewichtskraft Fg der angehängten Masse.

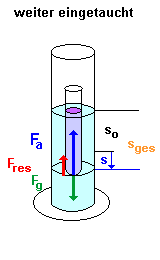
Wird das Reagenzglas weiter eingetaucht - und verdrängt daher mehr Wasser - so wird die Auftriebskraft Fa größer als die Gewichtskraft Fg des Reagenzglases.

Es ergibt sich daher eine resultierende Kraft - entgegen der zusätzlichen Auslenkung - nach oben.

Diese ist der zusätzlichen Auslenkung proportional.

Wird die Masse losgelassen, so wird sie nach oben beschleunigt.

Es ergibt sich daher eine resultierende Kraft - entgegen der zusätzlichen Auslenkung - nach oben.

Diese ist der zusätzlichen Auslenkung proportional.

Wird das Reagenzglas losgelassen, so wird es nach oben beschleunigt.

Es gilt:

Es gilt:

Das Vorzeichen im rechten Teil der Gleichung berücksichtigt, dass die zusätzliche Verlängerung nach unten (negativ) erfolgt, die Beschleunigung aber nach oben (positiv) wirkt.

Das Vorzeichen im rechten Teil der Gleichung berücksichtigt, dass die zusätzliche Verlängerung nach unten (negativ) erfolgt, die Beschleunigung aber nach oben (positiv) wirkt.

zeitabhängige Gleichung :

Während der sich ergebenden Schwingung ändert sich die Auslenkung s, die resultierende Kraft Fres und damit die Beschleunigung a ständig, a(t) ist dabei die zweite Ableitung der s(t) Funktion.

Während der sich ergebenden Schwingung ändert sich die Auslenkung s, die resultierende Kraft Fres und damit die Beschleunigung a ständig, a(t) ist dabei die zweite Ableitung der s(t) Funktion.

Dabei ist D die Federhärte der Feder.

Man sieht, dass der umrahmte Ausdruck der Federhärte auf der linken Seiten entspricht, man nennt den Ausdruck hier Richtgröße D.

Lösung der Differenzialgleichung 2. Ordnung :

Der Lösungsansatz ist hier (Anfangsbedingungen!)

Der Lösungsansatz ist hier (Anfangsbedingungen!)

also :

also :

In die Differenzialgleichung eingesetzt, ergibt sich nach Kürzen:

In die Differenzialgleichung eingesetzt, ergibt sich nach Kürzen:

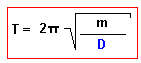
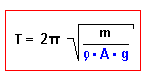
bzw. für die Periodendauer :

bzw. für die Periodendauer :