Lineare Bewegung und Schwingungsbewegung im Vergleich.

Die in den Diagrammen eingezeichneten Geradensteigungen sind kommentiert.
Fahre einfach mit der Maus über die Steigungspfeile!
Der Mauszeiger verändert sich dort zur Hand.

Die Ableitungen sind jeweils grau markiert und mit einer Nummer versehen.
Diese Nummern beziehen sich auf die Vergleichstabelle in "Physik trifft Mathematik - die Ableitungsregeln in Beispielen" im unteren Teil der Seite.
Solltest du die Ableitungen im oberen Teil nicht verstehen, so schaue sie dir im unteren Teil genauer an.
Die Farben helfen beim Verständnis.
Du kannst auf die Nummern klicken, dann springt die Seite automatisch nach unten.
Mit dem "Zurück" Knopf bist du dann wieder an der Ausgangsstelle.

	lineare Bewegung der Körper startet zum Zeitpunkt t = 0 s aus der Ruhe	Schwingungsbewegung es wird ein Start der Masse vom unteren Umkehrpunkt aus angenommen.
Ort	Weg-Zeit-Funktion: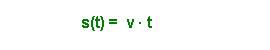	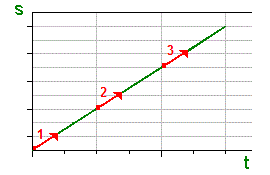Weg-Zeit-Funktion: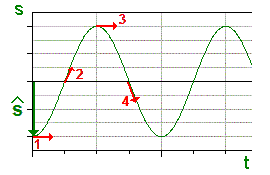
Geschwindigkeit	Die Momentangeschwindigkeit v(t) ist die Ableitung der Orts-Zeit-Funktion s(t) nach der Zeit. Es gilt: Mit einem Punkt über einer Größe bezeichnen die Physiker die Ableitung nach der Zeit, ein Strich ist - wie in der Mathematik - die Ableitung nach einer Ortskoordinate. Die erste Ableitung ist gleichzeitig auch die Steigung der Orts-Zeit-Funktion. (vgl. rote Einzeichnungen in den Diagrammen darüber)
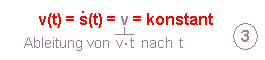
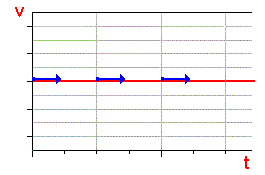
	Geschwindigkeits-Zeit-Funktion:	Geschwindigkeits-Zeit-Funktion: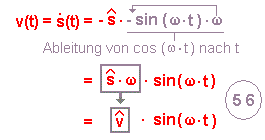
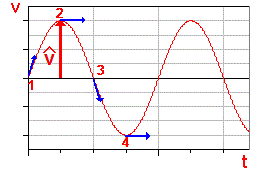
Beschleunigung	Die Momentanbeschleunigung a(t) ist die erste Ableitung der Geschwindigkeits-Zeit-Funktion v(t) nach der Zeit (oder die zweite Ableitung der Orts-Zeit-Funktion). Es gilt: 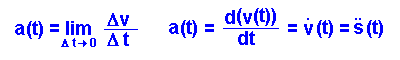Die zweite Ableitung ist gleichzeitig auch die Steigung der Geschwindigkeits-Zeit-Funktion. (vgl. blaue Einzeichnungen in den Diagrammen darüber)
	Beschleunigungs-Zeit-Funktion: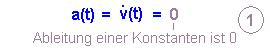	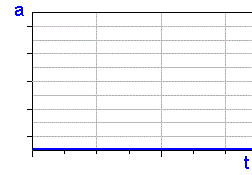Beschleunigungs-Zeit-Funktion: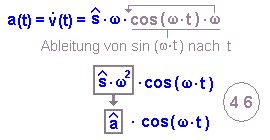

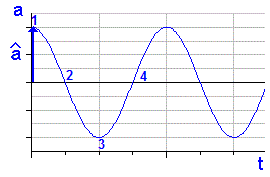Physik trifft Mathematik - die Ableitungsregel in Beispielen.

Oben wurden Ableitungen nach der Zeit t verwendet.
Dabei wurden die gleichen Regeln angewandt, wie du sie aus der Mathematik bei einer Ableitung nach x kennst.

Nummer	Regel	Formelsammlung		Beispiel aus der Physik
		Funktion	Ableitung nach x	Funktion	Ableitung nach t
1	Ableitung einer Konstanten			Geschwindigkeit konstant	Geschwindigkeitsänderung ist 0
2	Ableitung einer Potenzfunktion
3	Faktorregel: ein konstanter Faktor bleibt unverändert (schwarz)
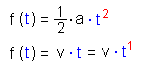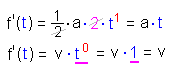4	Sinusfunktion
5	Kosinusfunktion
6	Kettenregel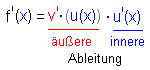

Zurück nach oben

Verwandte Seiten:

Lineare Bewegungen und Ableitungen im Vergleich. (Bereich Mechanik 2)

Grüninger, Landesbildungsserver, 2016