Lösungen zum Problem des Monats März 2025

PDM-Spirale

  1. Für das 7er-Quadrat braucht man 48 Buchstaben.
  2. Im 15er-Quadrat steht der Buchstabe D 75-mal.
  3. Nach dem 7er-Quadrat steht zunächst im 13er-Quadrat und anschließend im 19er-Quadrat in allen vier Ecken derselbe Buchstabe, jeweils M.

Erklärung:

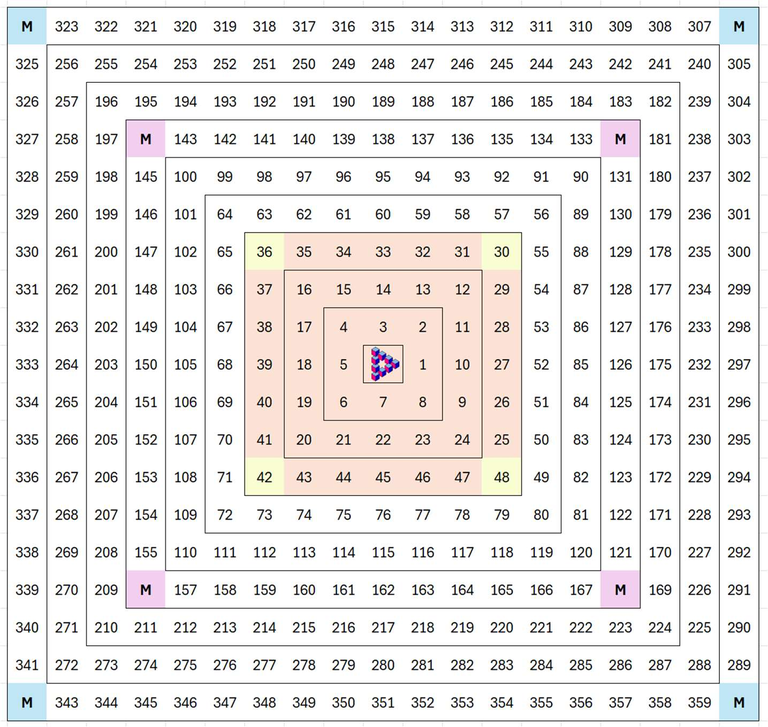
Gestaltet man die Spirale nicht mit den Buchstaben P, D und M, sondern nummeriert die Kästchen fortlaufend mit natürlichen Zahlen, so sieht man, dass die Zahl in der rechten unteren Ecke der Quadrate immer um eins kleiner ist als die entsprechende Quadratzahl der Anzahl der Kästchen der Seitenlänge.

Im 7er-Quadrat stehen 72-1 = 48 Buchstaben. Im 15er-Quadrat stehen 152-1 = 224 Buchstaben. Es ist 224:3 = 74 Rest 2, deswegen sind es 75-mal P, 75-mal D und nur 74-mal M.

Man kann beweisen, dass in allen vier Ecken derselbe Buchstabe steht, wenn die Anzahl der Kästchen der Seitenlänge des Quadrats um eins größer ist als eine durch sechs teilbare Zahl. Es handelt sich hierbei immer um den Buchstaben M, den dritten Buchstaben in PDM.

Abgebildet ist die PDM-Spirale bis zum 19er-Quadrat. Allerdings wurden die Buchstaben durch fortlaufende natürliche Zahlen ersetzt. Die Ecken des 7er-, 13er- und des 19er-Quadrats sind farbig markiert. Bis zum 7er-Quadrat hat die PdM-Spirale einen farbigen Hintergrund. Die Abbildung der PDM-Spirale ist für die Lösung nicht nötig, aber die beschriebenen Rechnungen werden so leichter verständlich.
Lizenz

Lösungen zum Download

Die Lösung zum Problem des Monats März als PDF Download [1,3 MB].
Interesse an weiteren Problemen des Monats? Archiv
Lizenz: (c) alle Rechte vorbehalten
Urheber: Autorinnen und Autoren des Problem des Monats

Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.