Die Lösung zum Problem des Monats Februar 2026
Zahlenkettchen
a) Lösungen:
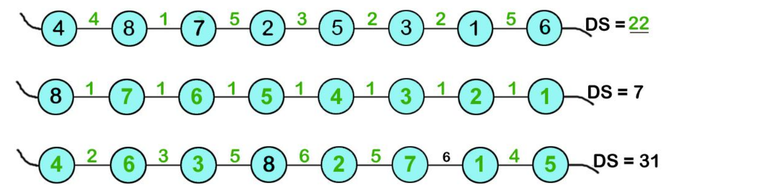
b) Nein, DS=31 ist nicht möglich, wenn die 8 ganz links steht.
Ja, DS=31 ist möglich, wenn die 8 an der 2. Stelle steht, zum Beispiel so:

Ja,DS=10 ist möglich, wenn die 8 an der 4. Stelle steht, und zwar so:

Erläuterungen:
Zu a) Für die 3. Graphik gibt es noch eine andere Möglichkeit, man kann die 3 und die 2 vertauschen.

Zu b) Für die Aufgabe „DS=31 und die 8 an der 2. Stelle“ gibt es insgesamt 12 Möglichkeiten. Alle beginnen mit 4 und enden auf 5.
Hinweis: Für eine beliebige Anordnung der acht Perlen gibt es insgesamt 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320 Möglichkeiten, 2 für die minimale Differenzensumme 7, 72 für die maximale Differenzensumme 31.
Die Lösung zum Problem des Monats Februar als PDF Download [531,8 kB].
Interesse an weiteren Problemen des Monats? Archiv
Lizenz: (c) alle Rechte vorbehalten
Urheber: Autorinnen und Autoren des Problem des Monats
Quelle:
Landesbildungsserver
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.


