Wichtige Grundfunktionen und ihre Graphen

Hinweise:

• Für den ersten Start der Animation benötigst du etwas Geduld.
• Der Begriff Graph kann auch durch den Begriff Schaubuld ersetzt werden
• Trenne immer den Funktionsbegriff von dem des Graphen. Eine lineare Funktion ist z. B. keine Gerade - der Graph einer linearen Funktion ist eine Gerade! Diese Trennung soll durch die verschiedenen Fenster verdeutlicht werden.
• Einige Funktionstypen besitzen Parameter (z. B. die Steigung und der y-Achsenabschnitt bei einer linearen Funktion). Die Parameter können in der Animation mit Schiebereglern verändert werden.
• Manche (Funktions-)Parameter (im linken Fenster) dürfen nicht mit beliebigen Zahlenwerten belegt werden. Finde Beispiele und begründe, warum es zu den Fehlermeldungen kommt.
• Im rechten Fenster kannst du einen Punkt mit der Maus (oder mit dem Schieberegler für den x-Wert) verschieben. Es gibt jedoch Funktionstypen, bei denen nicht zu jedem x-Wert ein Punkt auf dem Schaubild bestimmt werden kann. Finde Beispiele und begründe, warum es zu den Fehlermeldungen kommt.
• Für Interessierte:
  Zwischen bestimmten Funktionstypen gibt es eine besondere Beziehung. Diese zeigt sich u. a. durch Symmetrie der entsprechenden Graphen. (Vergleiche z. B. die Graphen der Quadratfunktion und Wurzelfunktion bzw. Exponentialfunktion und Logarithmusfunktion.)
  Der Graph der Kehrwertfunktion und die erste (und die zweite) Winkelhalbierende besitzen die gleiche Symmetrieeigenschaft bzgl. sich selbst.
  Wenn Du hier mehr wissen möchtest, musst Du dich mit dem Begriff "Umkehrfunktion" auseinandersetzten. Weitere Informationen hierzu findest Du im Netz.

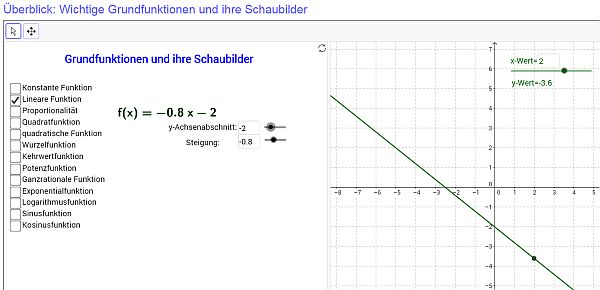
Dynamische Geogebra-Animation mit wichtigen Grundfunktionen und zugehörigen Graphen(Schaubilder).