Lineare Funktionen / Geraden
Lineare Zusammenhänge werden oftmals mit linearen Funktionen beschrieben. Zu jeder linearen Funktion gibt es eine Gerade, die den funktionalen Zusammenhang beschreibt. In der Regel werden die Geraden durch die Steigung und den y-Achsenabschnitt beschrieben. Mit diesen Werten lässt sich bei bekanntem Graphen auch die Funktionsvorschrift bestimmen.
Checkliste mit Diagnoseaufgaben, die zu passenden Lernvideos und/ oder Online-Übungen führen.

In Zeiten immer heterogener werdender Klassen gewinnen individualisierte Unterrichtsmethoden an Bedeutung.
Mithilfe dieser Checkliste können SchülerInnen selbstständig überprüfen, in welchen Teilgebieten sie noch Schwierigkeiten haben.
Um diesen adäquat zu begegnen, besteht einerseits die Möglichkeit, passende Lernvideos vom MINT-Preis-Gewinner Sebastian Stoll anzuschauen. Andererseits können die SchülerInnen individualisierte Übungen über einen QR-Code bearbeiten. Damit ist der Einsatz dieses Materials auch für Tablet-Klassen geeignet.
Ebenso erprobt ist der Einsatz für die Klassenarbeitsvorbereitung oder als differenzierte Hausaufgabe.
Multiplayer-Pferderennen zum Thema Lineare Funktionen
Der Multiplayer- Pferderennen wird sicherlich Ihr Renner im PC-Raum oder im Einsatz auf Schülerhandys. Bis zu sechs Spieler können gleichzeitig im Wettbewerb gegeneinander antreten und ihr bisheriges Verständnis testen. Besonders geeignet ist das Spiel nach dem Einsatz der Stationenarbeit zum Einstieg ins Thema. Lässt man kleine Gruppen gegeneinander antreten, so muss man als Spieler vorab seine Gruppenmitglieder mit guten mathematischen Argumenten überzeugen.
Animierte Übungsaufgabe: Zuordnungsvorschriften zu linearen Funktionen (Geradengleichungen bestimmen
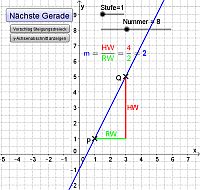
Die Animation zeigt eine Vielzahl von Geraden in drei Schwierigkeitsstufen. Hierbei kann der Lernende mit zwei verschiebbaren Hilfspunkten ein Steigungsdreieck "anpassen", so dass mit dem zugehörigen y-Achsenabschnitt die entsprechende Geradengleichung (Zuordnungsvorschrift) aufgestellt werden kann.
In der dritten Stufe kann man den y-Achsenabschnitt nicht direkt ablesen. Mit Hilfe der Steigung und einem gut sichtbaren Punkt lässt er sich aber recht einfach bestimmen. Eine Formel ist hierfür nicht notwendig - wird aber von fixen Schülern intuitiv gefunden.
Die Rechnungen können mit Hilfe von zwei Schaltflächen für Steigung und y-Achsenabschnitt selbstständig kontrolliert werden.
Zur interaktiven Geogebra-Animation
Die Gerade als Schaubild von linearen Funktionen
Schrittweise erklärt Mirjam Bartberger vom Gymnasium Karlsbad in ihrer Flash-Animation die Vorgehensweise beim Zeichnen einer Geraden zu einer gegebenen linearen Zuordnungsvorschrift.
Flash-Animation: Gerade zu einer linearen Zuordnung zeichnen
Rechenvorschrift aus Tabellenwerten bestimmen (und umgekehrt)
Das hier vorgestellte Arbeitsblatt ist für eine Klassenstufe 6 zum Thema Terme mit einer Variablen entstanden. Da die Kinder in diesem Alter den Zuordnungsbegriff noch nicht kennen, wurde dieser durch den Ausdruck "Rechenvorschrift" ersetzt.
Dokument-Download als OpenOffice- und als PDF-Datei
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Dominosteine zur Proportionalität, Antiproportionalität und linearen Zuordnung
Funktionale Zusammenhänge lassen sich auf vier verschiedene Weisen darstellen:
- Darstellung durch eine Funktionsgleichung
- Darstellung mit einem Schaubild im Achsenkreuz
- Tabellarische Darstellung mit ausgewählten Zahlenpaaren
- Darstellung in Textform beispielsweise in einer Sachaufgabe.
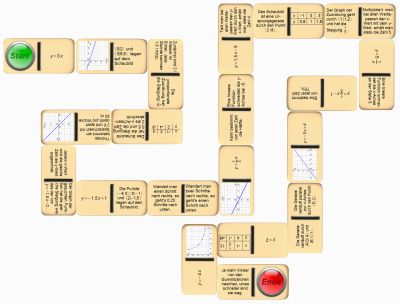
Mit dem nachfolgenden Domino-Puzzle soll das „Übersetzten“ von einer Zuordnungsform in eine andere spielerisch geübt werden. Jede Zuordnung taucht im Dominospiel in zwei verschiedenen Darstellungen auf. Hierdurch ergibt sich eine Reihenfolge für die Aneinanderreihung der Steine vom „Start“ bis zum „Ende“.
Dokument-Download als OpenOffice- und als PDF-Datei
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.




