Die kinetische Energie.
1.) Die Lageenergie - Wiederholung aus dem Anfangsunterricht.
Die Lageenergie ist um so größer, je
- größer die angehobene Masse m ist,
- größer die Höhe h ist, um die die Masse angehoben wurde,
außerdem spielt die Fallbeschleunigung g (auch Ortsfaktor genannt) eine Rolle.
| Für die Lageenergie gilt: |
Wenn dir dies nicht mehr klar ist, dann sieh dir diese Seite an: ;Lageenergie
2.) Energieerhaltung beim Freien Fall.
Die Kugel wurde um eine bestimmte Höhe hmax über dem
Nullniveau (z.B. Boden) angehoben. Sie wird von dort frei fallen gelassen.
Welche Energieumwandlungen passieren dabei?
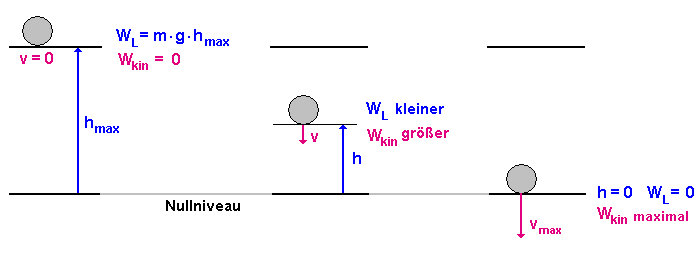
Beim Fallen
kommt die Kugel dem Boden immer näher, ihre Höhe h nimmt
ab, also wird auch ihre Lageenergie WL immer
kleiner.
Dafür wird die Kugel aber schneller,
d.h. ihre Geschwindigkeit v und ihre Bewegungsenergie nehmen
zu.
Man nennt die Bewegungsenergie auch kinetische Energie
Wkin (Kino - Ort, wo Filme, also bewegte Bilder gezeigt
werden).
Wir stellen die Energien aus dem linken Bild (oben) und dem
rechten Bild (unten) zusammen:
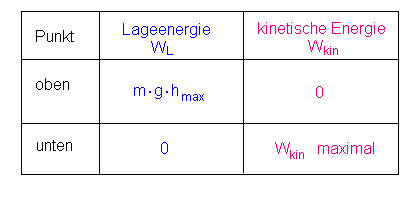
Nach dem Energieerhaltungssatz bleibt die
Gesamtenergie, also die Summe der beiden Energie WL und
Wkin, konstant: |
3.) Zusammenhang zwischen kinetischer Energie und Geschwindigkeit des Körpers.
Es ist klar, dass ein Körper nur dann kinetische Energie hat, wenn er
sich auch bewegt, d.h. wenn seine Geschwindigkeit v nicht 0 ist.
Es ist auch klar, dass die kinetische Energie dann groß sein wird, wenn
sich der Körper schnell bewegt, wenn seine Geschwindigkeit also groß
ist.
Aber wie genau ist nun der Zusammenhang zwischen Geschwindigkeit v und
kinetischer Energie Wkin und was spielt sonst noch eine Rolle?
Die Bewegungsgleichungen des Freies Falls lauten:
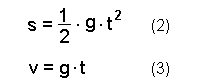
Löst man (3) nach der Zeit t auf und quadriert diese Gleichung so
ergibt sich:
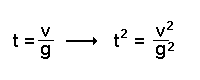
Dies kann man nun in die Gleichung (2) einsetzen und einmal mit g
kürzen.
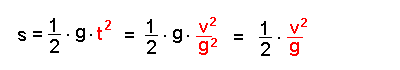
Setzt man dies dann noch in den Energieerhaltungssatz (Gleichung 1) ein so
folgt:
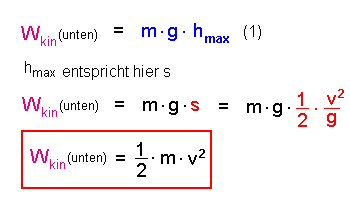
Mit anderen Worten:
- die kinetische Energie ist proportional zum Quadrat der
Geschwindigkeit - ist ein Körper doppelt so schnell, dann hat er
vierfache kinetische Energie.
- Die Masse des Körpers spielt dabei auch noch eine Rolle - aber das hatten wir uns ja fast gedacht.
4.) Interaktives Java-Applet zur Energieerhaltung beim freien Fall.
Arbeite die Fragen und Aufgaben unter dem Applet Schritt für Schritt durch, dann wirst du ein ganz gutes Gefühl für den Energieerhaltungssatz beim freien Fall bekommen. Vom Luftwiderstand wird abgesehen. Für die Fallbeschleunigung ist hier g = 10 m/s2 angesetzt.
5.) Fragen und Aufgaben:
5.1. Energien und Gleichung für kinetische Energie.
Belasse zunächst alle Grundeinstellungen und klicke einfach "Start".
- Wie verändern sich Lageenergie und Bewegungsenergie während der
Fallbewegung?
- Mit welcher Geschwindigkeit kommt die Kugel unten an?
Rechne mit dem Energieerhaltungssatz und der Gleichung von oben nach!
(für g ist hier 10 m/s2 bzw. 10 N/kg angenommen).
5.2. Vertiefung Energien, Zeiten, Geschwindigkeiten
Belasse zunächst alle Grundeinstellungen und klicke wieder "Start". Du kannst mit den Tasten "Schritt" die Simulation in 5 ms-Schritten vor und zurück laufen lassen.
5.2.1. Beide Energieformen sind gleich groß.
- Bei welcher Höhe sind Lageenergie und Bewegungsenergie gleich
groß?
Kannst du dies begründen?
- Warum ist in der halben Höhe die Geschwindigkeit nicht halb
so groß wie unten?
- Warum wird diese Höhe nicht nach der halben Fallzeit
erreicht?
5.2.2. Energien bei halber Endgeschwindigkeit.
- Wann hat die Kugel die halbe Endgeschwindigkeit (also 2,0 m/s)?
- Warum entspricht die zugehörige kinetische Energie 1/4 der Anfangsenergie?
- Wie groß ist die Lageenergie in dieser Höhe?
- Was kann man über die Gesamtenergie sagen?
5.3. Veränderung von Masse und Fallhöhe.
5.3.1. Veränderung der Masse.
Ändere nun mit den Auswahlfeldern die Masse auf 0,05 kg. Belasse die Starthöhe bei 0,8 m.
- Warum hat die Kugel nun nur noch halbe Lageenergie?
- Warum ist die Auftreffgeschwindigkeit am Boden trotzdem immer noch 4,0
m/s?
Begründe! - Was kannst du über die Zusammensetzung der Energien in 0,6 m Höhe
über dem Boden aussagen?
Vergleiche mit vorher!
5.3.2. Veränderung der Starthöhe.
Die Masse ist nun wieder 0,1 kg. Wähle als Starthöhe aber nun 0,4 m.
- Bei welcher Höhe sind die Energien gleich groß?
- Vergleiche mit deinen Ergebnissen aus 5.2.1. und kommentiere.
6. Zusätzliche Materialien zur Seite:
Arbeitsblätter im Format MS-Word:
Arbeitsblatt:
Der freie Fall - energetisch betrachtet. ![]()
Fragen und
Aufgaben zum Applet ![]()
Arbeitsblätter als PDF Dokumente:
Arbeitsblatt:
Der freie Fall - energetisch betrachtet. ![]()
Fragen und Aufgaben zum
Applet ![]()
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
(Copyright Hinweise) |


