Lineares Wachstum

Beim linearen Wachstum nimmt ein Bestand in jedem Zeitschritt um den gleichen Wert zu oder ab. Das kann beispielsweise ein Geldbetrag in einer Spardose sein, in der zu "Beginn der Zeitrechnung" ein Grundbetrag eingeworfen wurde und wöchentlich ein fester Sparbetrag hinzu kommt.
Den Begriff "linear" kennen wir vom linearen Gleichungssystem, der lineare Funktion oder der linearen Gleichung. In unserem Zusammenhang kommt die "Bestandsvariable" (oft t) nur mit der Hochzahl 1 vor (statt t^1 schreiben wir natürlich nur t).

Explizite und rekursive Wachstumsformel des linearen Wachstums

Für Berechnung des Bestandes nach t Zeitschritten gibt es zwei Möglichkeiten:

1. Bei der so genannten expliziten Methode kannst du den Bestand zu jedem beliebigen Zeitpunkt mit einer einzigen Rechnung bestimmen. Hierfür müssen allerdings der Anfangsbestand (B(0)) und der Zuwachs pro Zeitschritt (m) (bzw. die Abnhame pro Zeitschritt) bekannt sein. Die zugehörige explizite Formel lautet:

   B(t)=B(0)+m*t

2. Bei der rekursiven Wachstumsvorschrift "springt" man schrittweise von einem Bestand zum nächsten. Sie lautet:

   B(t+1)=B(t)+m

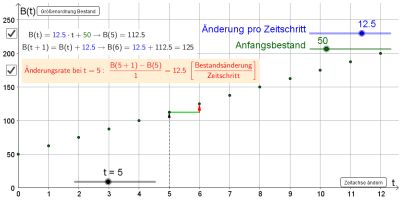
Animation zum grafischen Verlauf beim linearen Wachstum

Die Änderungsrate

Unter der Änderungsrate verstehen wir in der Mittelstufe die Geschwindigkeit, mit der sich ein Bestand ändert. Als Mathematiker drücken wir das mit der absoluten Änderung pro Zeitschritt aus.

Beim linearen Wachstum ist die Änderungsrate konstant. In unseren Wachstumsformeln ist die Änderungsrate exakt der Wert m.

Im obigen "Spardosen-Beispiel" wählen wir als Zeitschritt eine Woche. Damit entspricht der wöchentliche Sparbetrag unserer konstanten Änderungsrate.