Die hessesche Abstandsformel
Wir weisen auf dem downloadbaren Arbeitsblatt nach, dass mit der nachfolgenden Formel der Abstand eines Punktes R zu einer Ebene E im Raum berechnet werden kann:
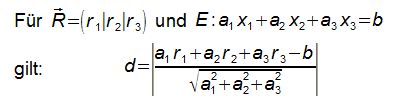
Notwendiges Vorwissen
- Kenntnis der Darstellung von Ebenen in Koordinatenform und in der hesseschen Normalenform.
- Darstellung von Richtungsvektoren mit Hilfe von Ortsvektoren.
- Skalarprodukt mit Hilfe der Vektorlängen und dem Kosinus des eingeschlossenen Winkels.
- Gleichheit von Wechselwinkel an Parallelen.
- Kosinusbeziehung am rechtwinkligen Dreieck.
- cos alpha= - cos (180°-alpha)
Hinweise zum Arbeitsblatt
- Das notwendige Grundwissen, sowie den Beweis der HNF-Formel mit Beispielen und weiteren Hinweisen können Sie auch in einem Lernvideo betrachten (allerdings mit der Kosinus-Definition am Einheitskreis).
- Das Dokument liegt im editierbaren OpenOffice- sowie im PDF-Format vor.
Dokument-Download als OpenOffice- und als PDF-Datei
Dokument als OpenOffice-Datei Download
Dokument als PDF Download
Lernvideo Teil 1: Abstand Punkt Ebene mit Lotfußpunkt
Zum Lernvideo 2: "Ebenenbestimmung mit vorgebenem Abstand"
Youtube-Lernvideo Teil 3: HNF-Abstandsformel - Grundlagen, Beweis sowie Anwendungen mit Hinweisen



