Hauptseite "Gleichungen"

Gleichungen spielen in der Mathematik eine hervorgehobene Rolle. Beim Abstrahieren von Alltagsproblemen in die Welt der Mathematik müssen regelmäßig Gleichungen aufgestellt und gelöst werden. Welche Gleichungsarten gibt es, und wie löst man sie?

Gleichungen

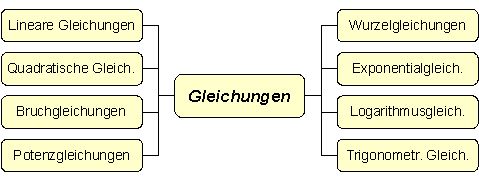
1. MindMap mit einem Überblick der (bis zum Abitur) relevanten Gleichungsarten

Klicke in der MindMap auf die jeweilige Gleichungsart, dann öffnet sich eine Seite mit Informationen zum jeweiligen Gleichungstyp.

2. Grafische Lösung von Gleichungen durch Schnitt zweier Schaubilder

Jede Seite einer Gleichung (mit einer Variablen) kann man auch als Funktion mit einem zugehörigen Schaubild interpretieren. Die Lösung der Gleichung läuft somit auf die Überlagerung zweier Schaubilder heraus. Schneiden sich diese Schaubilder, so sind die x-Werte der Schnittpunkte die Lösungen der Gleichung.

Bei dieser Vorgehensweise leisten grafikfähige Taschenrechner, CAS-Rechner oder Computerprogramme wie GeoGebra oder der Funktionsplotter von Arndt Brünner gute Dienste. Link zum Funktionsplotter von Arndt Brünner

Unter grafisches Lösen von Gleichungen mit GeoGebra erfährst du anhand verschiedener Beispiele, wie Gleichungen mit GeoGebra grafisch gelöst werden können.

3. Gleichungen aufstellen

In der Mathematik überträgt man Probleme aus dem Alltag in die "abstrakte" Welt der Zahlen und Variablen. Mit Hilfe der gültigen Rechengesetze lassen sich die so entstandenen Terme vereinfachen und gefundene Gleichungen lösen. Die "Rückübertragung" der Lösungen entspricht in der Regel auch der Lösung des Alltagsproblems.

Hierbei ist es hilfreich, wenn man bereits der Aufgabenstellung entnehmen kann, auf welche Art von Gleichung die Lösung hinaus läuft. Allerdings ist hierfür regelmäßiges Üben und wiederholen erforderlich. Unter Musteraufgaben findest du verschiedene Musteraufgaben mit ausführlichen Lösungen - nach Gleichungsarten sortiert.

4. Lösungstechniken

• Zu fast jedem der oben aufgeführten Gleichungstypen gibt es eine eigene Lösungtechnik. Diese Techniken müssen sorgfältig geübt und regelmäßig wiederholt werden.
• Bevor eine Lösungstechnik angewendet werden kann, müssen manche Gleichungen zunächst durch geeignete Umformungen in einen im obigen MindMap beschriebenen Typ umgewandelt werden. So führen gelegentlich Bruchgleichungen, Expoenentialgleichungen oder trigonometrische Gleichungen über das Verfahren der Substitution auf gewöhnliche quadratische Gleichungen. (Anschließend darf die Rücksubstitution nicht vergessen werden).
• Bei Gleichungsumformungen werden auf beiden Seiten der Gleichung die gleichen Rechenoperationen durchgeführt. Diese Regeln gelten nicht für Termumformungen!

Gleichungssysteme

Sucht man Werte für mehrere Variablen, so liefert das Lösen von Gleichungssystemen eine wertvolle Hilfe. Hierfür bieten sich drei Lösungsverfahren an. Ein Einsatz des GTR oder eines CAS ist in diesem Zusammenhang hilfreich.

Unsere Lernumgebung zu linearen Gleichungssystemen enthält eine Vielzahl an Materialien, insbesondere Lernvideos zum Additionsverfahren und zu besonderen Aufgabentypen bei linearen Gleichungssystemen.

Unterrichts- und Übungsmaterialien zu Gleichungssystemen

Hinweis:

Die Mathematik-Redaktion freut sich über weitere Aufgabenstellungen zur Veröffentlichung an dieser Stelle. (Kontaktadresse siehe unten links)