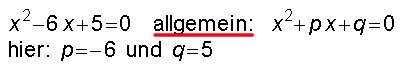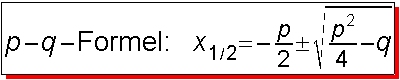Gemischtquadratische Gleichungen

Dieser Typ von quadratischen Gleichungen zeichnet sich dadurch aus, dass vor dem Quadrat der Variablen der Vorfaktor 1 steht. (Den Faktor 1 darf man natürlich auch weg lassen.)

Oft werden gemischtquadratische Gleichungen auch als normierte quadratische Gleichungen bezeichnet. Der Ausdruck quadratische Gleichung in Normalform entspricht diesem. Gelegentlich stößt man auch auf den Begriff "p-q-Form", welcher von dern üblichen Variablenbenennungen bei diesem Typ abstammt.

Jede allgemeine quadratische Gleichung kann mit einer beliebigen Zahl ungleich null multipliziert werden, ohne dass sich ihre Lösungen ändern. Dies hat zur Folge, dass es unendlich viele Darstellungen einer einzigen "Gruppe" von Gleichungen (mit gleichen Lösungen) gibt - aber nur eine gemischt quadratische in jeder dieser Gruppe.

Multipliziert man allgemeine quadratische Gleichungen aus solch einer Gruppe mit dem Kehrwert des Vorfaktors vor dem Quadrat der Variablen, so führen alle Gleichungen einer Gruppe zur gleichen gemischt quadratischen Gleichung. Diese ist durch die Zahl p (vor dem x) und die Zahl q ("ohne x") eindeutig festgelegt (normiert).

Beispiel:

Lösungstechnik:

Gemischtquadratische Gleichungen löst man mit der p-q-Formel (auch kleine Mitternachtsformel):

Beispiel 1:
(Tipp: Schau dir in diesem Zusammenhang auch das Lernvideo zum Lösen von quadratischen Gleichungen mit der p-q-Formel in der rechten Randspalte an.)

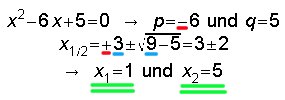
Beispiel 2:

(Allgemeine quadratische Gleichung in gemischtquadratische Gleichung zur Lösung mit der p-q-Formel überführen.)

Beachte die folgenden Tipps:

Wenn p negativ ist, ist -p/2 natürlich positiv (Bsp.1 rot). Versuche, diesen Schritt ohne Verwendung von Klammern gleich hinzuschreiben. (Falls p ein Bruch ist, verdoppelt sich bei -p/2 der Nenner. Eventuell kann man noch kürzen.)
Das Rechenzeichen in der Wurzel ist genau dann ein Pluszeichen, wenn q negativ ist.
Die erste Zahl in der Wurzel ist stets das Quadrat der Zahl vor der Wurzel ( Bsp. 1 blau). Hierbei spielt das Vorzeichen von p keine Rolle. (p^2/4 ist immer positiv !)
Erweiterer q in der Wurzel gleich auf den richtigen Nenner, so dass anschließend gleich addiert / subtrahiert werden kann.
Der Ausdruck unter der Wurzel heißt Diskriminante (D). Die Diskriminante entscheidet, ob die Gleichung genau zwei Lösungen hat (D>0), überhaupt keine Lösung besitzt (D<0) oder ob die Gleichung eine eindeutige Lösung hat (D=0).
Bei manchen (schwierigeren) Aufgaben mit Parametern kann man mit diesem Wissen den Parameter bestimmen, wenn die Gleichung genau eine Lösung besitzen muss. Man findet den Wert des Parameters in diesem Fall über die Forderung D=0.