Berechnung von P
1. Darstellung von Anteilen
Beispiel 1: Anteile von 1 Meter
Du kennst inzwischen drei Möglichkeiten Anteile darzustellen:
1. Als Prozentanteil 40% von 1m
2. Als Bruchteil 40/100 m= 4/10 m = 2/5 m
3. In Dezimalschreibweise 0,40 m
2. Die Berechnung von Anteilen
Somit stehen dir auch für die Berechnung drei Wege zur Verfügung.
Beispiel 2: Anteile von 15 €
a) Bruchrechnung
Beim Bruchrechnen berechnet man Bruchteile von Größen mit Hilfe der Multiplikation. Das Wort "von" im Text wird zum Rechenzeichen "mal" in der Rechnung.
Bsp.: 2/5 von 15€= 2/5 * 15 € = 6 €
b) Prozentrechnung mit Hundertstelbrüchen
Beim Prozentrechnen verwendet man nur Hundertstelbrüche. 2/5 = 40/100. Der Rechenweg bleibt der gleiche.
Bsp.: 40% von 15 € = 40/100 * 15 € = 6 €
c) Prozentrechnung mit Dezimalzahlen / Prozenfaktoren
Die Tatsache, dass man jeden Hundertstelbruch im Kopf problemlos in eine Dezimalzahl umwandeln kann, vereinfacht die Rechnung mit dem Taschenrechner.
Bsp.: 40% von 15 € = 0,4 * 15 € = 6 €
Der Zusammenhang von Bruchzahl - Prozentsatz - Dezimalzahl (Prozentfaktor f)
| Bruchzahl | 1 100 |
5 100 |
10 100 |
25 100 |
40 100 |
| Prozentsatz p | 1 % | 5 % | 10% | 25% | 40% |
| Dezimalzahl/Prozentfaktor | 0,01 | 0,05 | 0,1 | 0,25 | 0,4 |
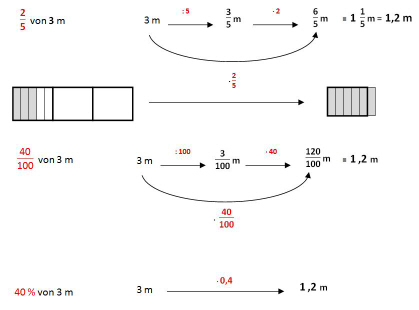
Beispiel 3 : 40% "von" 3m
Hier nochmal die 3 Möglichkeiten 40% von 3 m zu berechnen. 40% sind 40/100 oder gekürzt 2/5. Das Wort "von" wird in der Rechnung zu einer Multiplikation " * "
1. Man berechnet entweder 2/5 von 3m
2. oder 40/100 von 3m
3. oder 0,4 * 3m
Berechnung des Prozentwertes P mit dem Prozentfaktor f
Beispiel 4:
Um 4% von 150 @ mit dem Taschenrechner zu berechnen benötigt man :
- Eine Vorüberlegung: Die Umrechnung des Prozentsatzes in eine Dezimalzahl ( Bsp. p = 4% >>> f = 0,04)
- Die Multiplikation der Dezimalzahl f mit dem Grundwert G
Verwendet man bei der Berechnung des Prozentwertes den Prozentfaktor f, kann man den Prozentwert P durch eine einfache Multiplikation berechnen.

4% von 150 € = 0,04 * 150 = 6,00 €
Berechne die fehlenden Prozentwerte . Kontrolliere deine Lösungen mit dem Applet.
| Grundwert G | 150 @ | 250 @ | 300 @ | 400 @ | 800 @ | 900 @ |
| Prozentsatz p | 4 % | 4 % | 15 % | 15 % | 60 % | 60 % |
| Prozentwert P |
Das Kreis- und Streifendiagramm dienen zur Veranschaulichung und Kontrolle der Lösungen
Du kannst mit den beiden Schiebereglern den Grundwert G und den Prozentsatz p so ändern, dass er mit den Tabellenwerten übereinstimmt. Das Laden des Applets kann etwas dauern.



