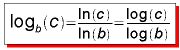Hauptseite Exponentialgleichungen

Exponentialgleichungen löst man (in der Regel) durch Logarithmieren.

Nur mit dem Logarithmus können wir bei einer Exponentialgleichung die Variable im Exponenten einer Potenz berechenbar machen. Hier bekommt der Logarithmus seine "Existenzberechtigung". Interessanterweise wird der Logarithmus sogar als Lösung einer Exponentialgleichung definiert. Logarithmus bei www.wikipedia.de

Besonderheiten bei Exponentialgleichungen

• Ähnlich wie beim Quadrieren von Wurzelgleichungen muss man auch hier darauf achten, dass die Potenz alleine auf einer Seite der Gleichung steht. Eventuelle Vorfaktoren verursachen Probleme und sollten daher vor dem Logarithmieren auf die anderer Seite der Gleichung geschoben werden.
• Potenzen mit positiver Basis sind stets positiv. Daher erkennt man auf den ersten Blick, wenn eine (einfache) Exponentialgleichung unlösbar ist. (Musteraufgabe 2)
• Tauchen mehrere Potenzen mit der Lösungsvariablen in der Hochzahl aus, besteht die Möglichkeit der Vereinfachung durch Ausklammern.
• Bei einem speziellen Typ von Exponentialgleichungen führt eine Substitution zu einer quadratischen Gleichung.
• Bestimmte Exponentialgleichungen sind mit den Mitteln der Schulmathematik nicht exakt lösbar. Als letzter Ausweg bleibt dann nur die grafische Lösung oder die (etwas mühsame) Intervallschachtelung.
• In den meisten (einfachen) Fällen führt eine Expoenentialgleichung nach dem Logarithmieren auf die Lösung x = log_b(c). Hierbei stehen die Variablen b und c für zwei positive, reelle Zahlen. Leider besitzt unser Taschenrechner nur Funktionstasten für den natürlichen Logarithmus ln (Basis ist hier die Eulersche Zahl e) und den Logarithmus zur Basis 10 (log). Logarithmen beliebiger Basen lassen sich aber leicht mit einer dieser Funktionstasten (näherungsweise) berechnen (vgl. Musteraufgabe 1):
  
  "Taschenrechner-Formel" für Logarithmus mit beliebiger Basis b: