Logarithmusgleichungen
Logarithmusgleichungen spielen in der Schulmathematik keine große Rolle. Eine ausführührliche Behandlung der Logarithmusgleichungen setzt die Kenntnis der Logarithmusgesetzte voraus. Dies würde hier zu weit führen.
Grundlegend ist folgendes zu beachten:
- Da der Logarithmus nur für positive Zahlen definiert ist, muss man bei Logarithmusgleichungen die Definitionsmenge bestimmen.
- Logarithmusgleichungen löst man durch "exponieren" (= Anwenden einer Exponentialfunktion auf beide Seiten der Gleichung).Hierbei nutzt man aus, dass der Logarithmus über eine Exponentialgleichung definiert ist. Somit liefert die Potenz mit einem Logarithmus im Exponenten (bei richtiger Wahl der Basis) gerade das Argument des Logarithmus als Ergebnis.
- Die Wahl der Basis beim Exponieren richtet sich nach der Basis des Logarithmus. Steht beim Logarithmus log keine Basis, so gilt nach einer allgemeinen Vereinbarung innerhalb eines schulischen Kontext die Basis 10. Wird der Logarithmus mit ln abgekürzt, bezeichnet diese Abkürzung den natürlichen Logarithmus (mit der Eulerschen Zahl e als Basis).
- Grundsätzlich kann man jeden Logarithmus mit einem besseren Taschenrechner in ein Produkt aus Vorfaktor und Logarithmus zur Basis 10 umwandeln. Leider steht die hierfür benötigte "Taschenrechner-Formel" nicht in den üblichen Formelsammlungen.
Musteraufgabe (in 2 Versionen):
Version 1 (Standardlösung):
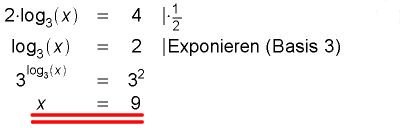
Version 2 (mit "Taschenrechner-Formel"):




