Allgemeine quadratische Gleichungen
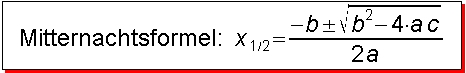
Allerdings liegen die Gleichungen in der Regel nicht so vor, dass man die Mitternachtsformel direkt anwenden kann. Damit die Gleichung "reif für die Mitternachtsformel" ist gehe folgendermaßen vor:
- Entferne Klammern und "räume die Gleichung so auf", dass auf der einen
Seite null steht.
- Fasse auf der anderen Seite gleichartige Summanden zusammen und sortiere nach x-Potenzen (die mit x^2, die mit x und die "ohne x").
Beispiel:

Beachte die folgenden Tipps:
- Der Ausdruck unter der Wurzel heißt Diskriminante. Die erste
Zahl ist als Quadrat niemals negativ.
Das anschließende Rechenzeichen ist genau dann ein "+" wenn die Zahlen für a und c verschiedene Vorzeichen haben. - Vergiss nicht, das Doppelte der Zahl a unter dem Bruchstrich. Da a in vielen Fällen 1 ist (und weggelassen werden kann) wird es oft vergessen, wenn es nicht 1 ist.
- Genau dann wenn die Diskriminante negativ ist, hat die Gleichung keine
Lösungen. Wenn b^2=4ac ist die Diskriminante 0. In diesem Fall gibt es
genau eine Lösung.
- Alternativ lässt sich die allgemeine quadratische Gleichung durch
beidseitige Multiplikation mit dem Kehrwert des Vorfaktors vom
quadratischen Ausdruck in die gemischtquadratische Form überführen. Auf
diese Art umgeht man die (etwas komplizierterer) Mitternachtsformel und
kann die Aufgabe mit der p-q-Formel lösen. Siehe Lösung der
Beispielaufgabe mit p-q-Formel.
Linktipp:
Hier kannst Du am Computer gemischtquadratische Gleichungen mit der p-q-Formel und allgemeine quadratische Gleichungen mit der Mitternachtsformel lösen.Programm für Lösungsformeln



