Quadratische Gleichungen, bei denen die Variable ausschließlich in der ersten oder zweiten binomischen Formel erscheint
Beispiele: 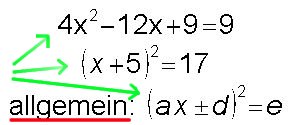
Beidseitiges Wurzel ziehen liefert schnell die entsprechenden Lösungen.
Beachte hierbei wieder, dass es auch negative Wurzeln Lösungen von
quadratischen Gleichungen sind.
Beispiel:

Nachdem man eine allgemeine quadratische Gleichung durch Normierung in eine gemischtquadratische Gleichung überführt hat, lässt diese sich immer durch quadratischen Ergänzung in die obige Form überführen.
Einfacher ist in solch einem Fall allerdings die Anwendung der jeweiligen Lösungsformel (für allgemeine bzw. gemischtquadratische Gleichungen).



