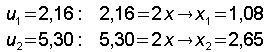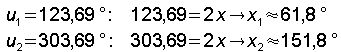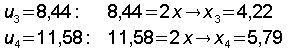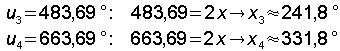Musteraufgabe Tangensgleichung
Musteraufgabe:
Bestimme alle Winkel innerhalb des Intervalls [0°, 360°) bzw. [0, 2*pi), die die folgende Gleichung lösen:
Lösung:
Diese Aufgabe besitzt zwei Schwierigkeiten:- Im Argument des Tangens steht statt x der Ausdruck 2x. Wir umgehen
diese Schwierigkeit zunächst (!) durch die Substitution u := 2x.
(Vergleiche hierzu die Bemerkung am Ende der Seite.)
- Der Tangens ist negativ. Dies führt dazu, dass der Taschenrechner einen negativen Winkel angibt, der in den Bereich der Grundmenge transformiert werden muss.
Mit der Substitution erhalten wir die Gleichung tan (u) = -1,5. Der
Taschenrechner liefert hierzu u = - 0,98 bzw. u = -56,31°. Beide Werte
lassen sich rück-substituieren:
Aus 2x = -0,98 folgt x = -0,49 (bzw. -28,16° im Winkelmaß) beide
Winkelwerte sind nicht in der Grundmenge enthalten.
Hier hilft uns wieder die Skizze mit dem Einheitskreis - dieses Mal mit der Veranschaulichung des Tangens:
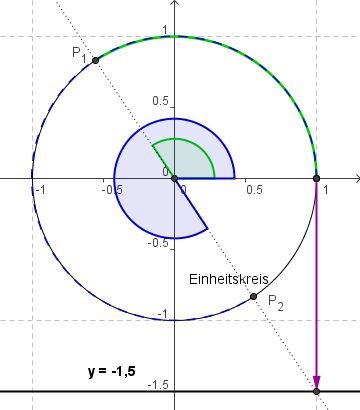
An der Skizze erkennt man, dass der (negative) Winkelwert des Taschenrechners den Punkt P1 beschreibt. Erhöht man den Winkelwert (für u) um einen Vollwinkel (2*pi bzw. 360°), trifft man wieder auf P1. Bei einer Erhöhung nur um pi bzw. 180°, gelangt man zu P2. Auch hier wird die (substituierte) Gleichung erfüllt. Und nun sind wir mit unseren Lösungen auch im Bereich der Grundmenge.
Ganz genau erkennen wir dies aber erst bei der Rücksubstitution. Zunächst liefern die Punkte P1 und P2 die Winkelwerte für u:
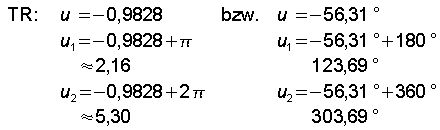
Kommen wir zur Rücksubstitution:
Im Bogenmaß:
Im Gradmaß:
Achtung:
Die Aufgabe ist noch nicht gelöst. An den Ergebnissen für x erkennt man, dass man mit u noch ein weiters Mal auf dem Einheitskreis "wandern" kann, ohne dass die Lösungen für x außerhalb der Grundmenge liegen. Wir gehen wieder in der obigen Reihenfolge vor:
Weitere Winkelwerte für u: 
Rücksubstitution:
Im Bogenmaß:
Im Gradmaß:
Nun liegen alle Lösungen innerhalb der Grundmenge. Wir können die
Lösungsmenge bestimmen.
Bemerkungen:
- Im Gegensatz zu den Lösungen bei Sinus- oder Kosinusgleichungen liegen bei den (einfachen) Tangensgleichungen die Lösungen stets in gleichen Abständen voneinander entfernt. Dies macht man sich am besten an den Schaubildern dieser Funktionen klar.
- Wenn bekannt ist, dass das Schaubild der Funktion g(x)=f(2x) aus dem Schaubild einer beliebigen Funktion f(x) durch "Streckung in x-Richtung mit dem Faktor 0,5" hervor geht, ist bei dieser Aufgabe die Lösung über das Schaubild der (gestreckten Tangensfunktion) deutlich einfacher als die oben vorgeführte.