"Faule" Lösungen bei Wurzelgleichung
"Quadrieren" ist keine Äquivalenzumformung. Da sich jedoch die
Lösungsmenge einer Gleichung beim Quadrieren schlimmstenfalls vergrößert,
hilft uns dieses Mittel bei der Suche nach Lösungen von Wurzelgleichungen.
Die "falschen" Lösungen müssen wir im Anschluss durch eine Probe wieder
herausfiltern.
Beispiel:
![]()
Zu Schritt 1: (Bestimmung der Definitionsmenge)
Die linke Seite der Gleichung ist für die Belegungen nicht definiert, bei denen der Radikant 6-x negativ ist. Dieser Fall tritt genau dann nicht ein, wenn x kleiner gleich 6 ist. Wir erhalten als Definitionsmenge:
![]()
Zu Schritt 2: (Lösen durch quadrieren)
Die Wurzel steht bereits alleine auf einer Seite, somit kann sofort quadriert werden:

zu Schritt 3: (Falsche Lösungen aussortieren)
Obwohl beide Lösungen in unserer Definitionsmenge enthalten sind, ist die Gleichung beim Einsetzen in einem Fall nicht erfüllt. Die falschen Lösungen werden somit durch Nachrechnen sofort enttarnt: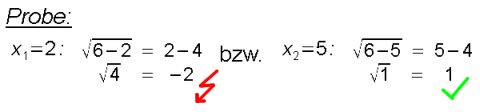
Ergebnis:
Aufgrund der Probe müssen wir eine Lösung "verwerfen". Wir erhalten als einzige Lösung unserer Wurzelgleichung die Zahl 5.
Hinweise:
- Durch Quadrieren kann man (fälschlicherweise) zeigen, dass -1=1 ist. Dies liegt natürlich daran, dass Quadrieren keine Äquivalenzumformung ist.
- Interessierte Mathematiker können sich auch mit der Aufgabe 4 der folgenden Aufgaben beschäftigen. Hier muss zweimal quadriert werden. Die Umformung der Summe in ein Produkt mag für viele "vom Himmel fallen" - mit einem Computer-Algebra-System (CAS) erfolgt dieser Schritt jedoch auf Knopfdruck. Die Aufgabe übersteigt das geforderte Niveau am Gymnasium, ist jedoch eine schöne Übung mathematische Wettbewerbe.



