Hauptnenner bestimmen
Beim Lösen der Bruchgleichungen spielt die Bestimmung des Hauptnenners eine wesentliche Rolle.
Wie schon bei der Addition von Brüchen ist nicht jeder gemeinsame Nenner automatisch der kleinste. Bei unseren Schülerinnen und Schülern führ dies gelegentlich dazu, dass die Gleichungen unnötig "aufgebläht" werden.
Gehe bei der Hauptnenner-Bestimmung mit einer (zwei- oder) dreispaltigen Tabelle vor:
- Schreibe alle vorkommenden Nenner in einer Spalte untereinander.
- Zerlege in der Spalte daneben die jeweiligen Nenner in ein Produkt mit möglichst vielen Faktoren.
- Tauchen bei den Nennern bekannte Faktoren aus einem anderen Nenner auf, schreibe sie darunter.
- Unterstreiche die Zeilen mit den Nennern und übertrage die vorkommenden Faktoren in ihrer größten "Vielfachheit" auf den Hauptnenner. (Im folgenden Beispiel hat der Faktor 2 die Vielfachheit 2, weil er im dritten Nenner doppelt auftritt.)
- Es macht keinen Sinn, die Faktoren im Hauptnenner wieder zusammenzufassen. Beim Durchmultiplizieren der Gleichung kürzen sich die Faktoren eh wieder heraus. Mit etwas Übung kann man so eine Zeile beim Umformen überspringen (siehe ausführliche Lösung unter dem Beispiel).
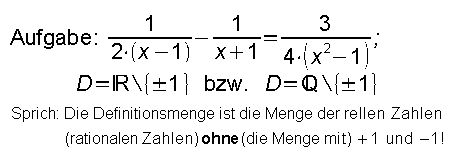
Beispiel:
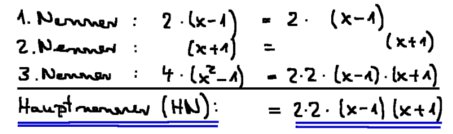
Ausführliche Lösung
Klicke hier, und es öffnet sich ein Fenster mit der ausführlichen Lösung. Die Farben schulen dein mathematisches Regelverständnis. Ihre Bedeutung wird bei den Termumformungen beschrieben.
Beachte, dass die Lösungen bei Bruchgleichungen mit der Definitionsmenge abgeglichen werden müssen (denn falls die Lösung einen Nenner null werden lässt, ist die Gleichung für diese Zahl gar nicht definiert).


