Die gemischt quadratische Gleichung
2. Die gemischt quadratische Gleichung mit Binom
Kommt die Variable in einer Gleichung in der 1. und 2. Potenz ( x und x² ) vor, nennt man sie "gemischt quadratische Gleichung".
( x + d )² = c ⇔ x² + 2dx + d² = c
Beispiel für d = 5 und c =64:
( x + 5)² = 64 ⇔ x² + 10x + 25 = 64
x = ?
Gemischt quadratische Gleichungen mit Binom löst man, indem man auf beiden Seiten der Gleichung die Wurzel zieht.
Beachte, dass auch diese Gleichung zwei Lösungen hat!
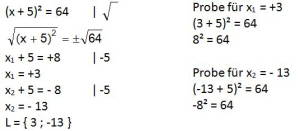
In dieser Gleichung kommt die Variable in der 1. binomischen Formel vor. Der Lösungsweg ist der Gleiche wie bei der rein quadratischen Gleichung.
Kommt die Variable nicht in der 1. binomischen Formel vor, kann man die "quadratische Ergänzung" durchführen.
Mithilfe der quadratische Ergänzung kann man eine Gleichung wieder auf die Form ( x + d )² = c bringen und so den oben beschriebenen Lösungsweg durchführen.



