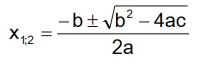Gemischt quadratische Gleichung
3. Die gemischt quadratische Gleichung der Form x² + px + q = 0
Beispiel : x² + 2x – 15 = 0
Gemischt quadratische Gleichungen löst man, indem man die Werte für p und q in die Lösungsformel einsetzt
Lösungsformel:
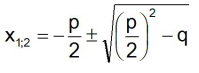
Die Herleitung der Lösungsformel kann man sich an folgenden Beispielen anschauen:
Lernpräsentation: Herleitung der Lösungsformel
Links zur Herleitung der Lösungsformel
Setzt man in die Lösungsformel für p = 2 und q = -15 ein erhält man die beiden Lösungen
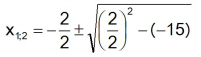
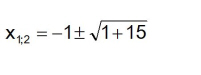
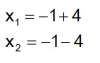
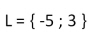
Die Diskriminante
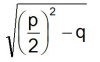
Diskriminieren bedeutet unterscheiden.
Um zu unterscheiden, ob eine quadratische Gleichung keine, eine oder zwei Lösungen hat, betrachtet man den Radikand (den Wert unter der Wurzel) in der Lösungsformel .
- hat der Radikand den Wert 0, dann hat die Gleichung eine Lösung
- ist der Radikand positiv, dann hat die Gleichung zwei Lösungen
- ist der Radikand negativ, dann hat die Gleichung keine Lösung
3.1. Die gemischt quadratische Gleichung der Form ax² + bx + c = 0
Steht bei dem x² ein Faktor a muss man die Gleichung durch a dividieren, wenn man die oben gezeigte Lösungsformel verwenden will.
Man kann aber auch diese Lösungsformel verwenden.