Die quadratische Ergänzung

Um eine beliebige gemischt quadratische Gleichung in die Form ( x + d )² = c zu bringen, muss man die quadratische Ergänzung durchführen.

1. Binomische Formeln ergänzen

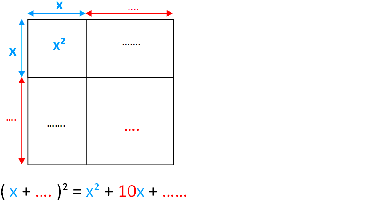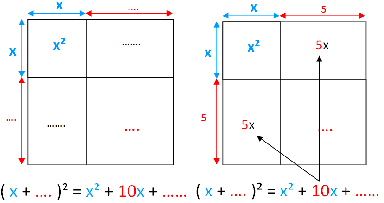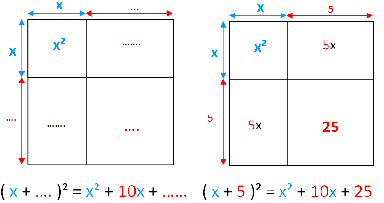
Beispiel: x² + 10x + ........

Bei diesem Beispiel fehlt das "zweite Quadrat". Kennt man das "erste Quadrat" und das "Doppelte Produkt", findet man das "zweite Quadrat", indem man

• das "Doppelte Produkt" halbiert 10x : 2 = 5x
• durch die die Variable dividiert 5x : x = 5
• diesen Wert quadriert 5² = 25

Die vollständige binomische Formel ist x² + 10x + 25 = ( x + 5 )²

Beispiel:

Lizenz

2. Die Quadratische Ergänzung bei einer gemischt quadratischen Gleichung

Beispiel: x² + 2x - 15 = 0

Der Term auf der linken Seite ist kein Binom. Jedoch ist x² + 2x Teil einer binomischen Formel. Ergänzt man in diesem Fall das "zweite Quadrat" erhält man die binomische Formel:

x² + 2x + 1 = (x + 1)².

Um eine gemischt quadratische Gleichung in die Form ( x + d )² = c zu bringen, muss man zuerst auf beiden Seiten der Gleichung das "zweite Quadrat" addieren,

Lizenz